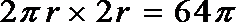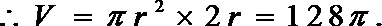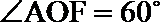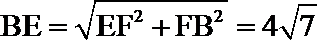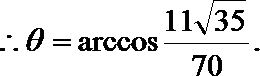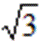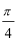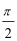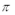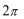三角函数的图象与性质
共601题

三角函数的图象与性质
共601题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

7 ．已知，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用运用诱导公式化简求值数列与三角函数的综合

题型：简答题

简答题 · 14 分

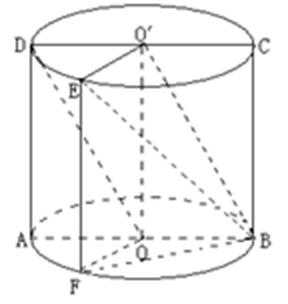
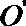
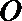
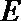
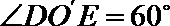
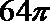
20．如下图，圆柱的轴截面为正方形，、分别为上、下底面的圆心，为上底面圆周上一点，已知，圆柱侧面积等于．

（1）求圆柱的体积；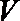

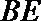
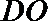
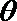
（2）求异面直线与所成角的大小．

正确答案

（1）设圆柱的底面半径为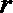，由题意，得

解得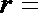：4．

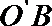
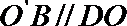
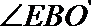
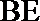
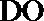
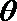
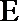
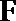
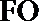
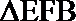
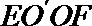
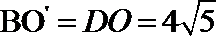
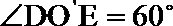
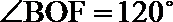
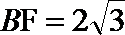
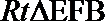
（2）连接，由于，所以，即为与所成角，过点作圆柱的母线交下底面于点，连接，，由圆柱的性质，得为直角三角形，四边形为矩形，

，由，由等角定理，得

所以，可解得，在中，

由余弦定理，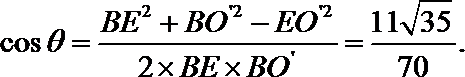

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法

题型：填空题

填空题 · 5 分

12．若，则 __________．

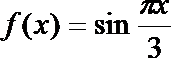
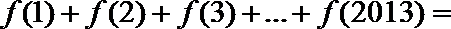
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法运用诱导公式化简求值分组转化法求和

题型：简答题

简答题 · 12 分

16．已知函数，．

（1）求函数的最小正周期和单调递增区间；

（2）若函数图象上的两点的横坐标依次为，为坐标原点，求的外接圆的面积．

正确答案

（1）

（2）

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的单调性三角函数中的恒等变换应用正弦定理余弦定理

题型：填空题

填空题 · 5 分

15．下列几个命题：

①方程有一个正实根，一个负实根，则；

②函数是偶函数，但不是奇函数；

③设函数定义域为R，则函数与的图象关于轴对称；

④一条曲线和直线的公共点个数是，则的值不可能是．

其中正确的有_______________．

正确答案

①④

解析

方程有一个正实根，一个负实根，

则当时，，

故，故①正确；

对于②，函数化为，是常函数，且其既为偶函数也为奇函数，故②错；

对于③，与的图象对称轴为，故③错；

对于④，和直线的公共点个数可以是不可能是，故④正确.

答案为：①④.

知识点

三角函数的周期性及其求法

题型：简答题

简答题 · 12 分

16．已知函数．

（1）求函数的最小正周期和最大值；

（2）在给出的平面直角坐标系中，画出函数在区间上的图像．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的图象三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 12 分

19．设函数，其中向量，向量.

（1）求的最小正周期；

（2）在中，分别是角的对边，，求的长．

正确答案

（1）因为

所以最小正周期是.

（2）由，解得三角形内角；

又由余弦定理得， ①

②

解①②得

或.

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用正弦定理余弦定理平面向量数量积的运算

题型：单选题

单选题 · 5 分

2．函数（）的最小正周期是，若其图像向左平移个单位后得到的函数为奇函数，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的奇偶性函数y=Asin（ωx+φ）的图象变换

题型：单选题

单选题 · 5 分

4．函数的最小正周期是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

16.已知向量函数

（I）求函数的解析式，并求其最小正周期；

（II）求函数图象的对称中心坐标与对称轴方程和单调递增区间.

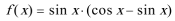
正确答案

解: （I）

（II）∵

令即得

∴对称点为

由得

∴对称轴方程为

∵的单调增区间∴递减，

∴

∴的单调递增区间是（开区间也对）

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用平面向量数量积的运算

继续学习学习下一知识点

下一知识点 : 三角恒等变换

百度题库 > 高考 > 文科数学 > 三角函数的图象与性质

扫码查看完整答案与解析