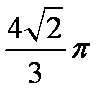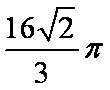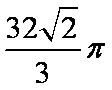如图(7)所示,已知A、B、C是长轴长为4的椭圆E
上的三点,点A是长轴的一个端点,BC过椭圆中心O,
且
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得
(3)过椭圆E上异于其顶点的任一点P,作

正确答案
见解析。
解析
(1)
依题意知:椭圆的长半轴长
设椭圆E的方程为
由椭圆的对称性知|OC|=|OB| 又∵
∴AC⊥BC,|OC|=|AC| ∴△AOC为等腰直角三角形,
∴点C的坐标为(1,1),点B的坐标为(-1,-1) ,
将C的坐标(1,1)代入椭圆方程得
∴所求的椭圆E的方程为
(2)解法一:设在椭圆E上存在点Q,使得

即点Q在直线
∴点Q即直线
∵直线


∴满足条件的点Q存在,且有两个。
【解法二:设在椭圆E上存在点Q,使得

即
又∵点Q在椭圆E上,∴
由①式得

∵方程③的根判别式
∴方程③有两个不相等的实数根,即满足条件的点Q存在,且有两个。
(3)解法一:
设点


∴O、M、P、N四点在同一圆上,且圆的直径为OP,则圆心为
其方程为
即
即点M、N满足方程④,又点M、N都在
∴M、N坐标也满足方程
⑤-④得直线MN的方程为
令



∴
∴

【解法二:设点
直线PM的方程为

同理可得直线PN的方程为
把P点的坐标代入④、⑤得
∴直线MN的方程为
令



∴
∴

知识点
已知函数
(1)证明:函数

(2)解关于x的不等式
正确答案
见解析
解析
(1)







(2)由


又


解得



知识点
今天你低碳了吗?近来,国内网站流行一种名为“碳排放计算器”的软件,人们可以用它计算出自己每天的碳排放量。例如:家居用电的碳排放量(千克)= 耗电度数×0.785,汽车的碳排放量(千克)=油耗公升数×0.785等。某班同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例数据如下:

(1)如果甲、乙来自A小区,丙、丁来自B小区,求这4人中恰有2人是低碳族的概率;
(2)A小区经过大力宣传,每周非低碳族中有20%的人加入到低碳族的行列。 如果2周后随机地从A小区中任选25个人,记
正确答案
见解析
解析
(1)记这4人中恰好有2人是低碳族为事件A,则
(2)设A小区有a人,2周后非低碳族的概率



知识点
四棱锥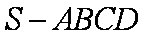
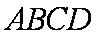
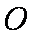
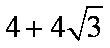
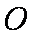
正确答案
解析
由题意可知四棱锥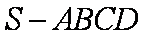
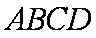
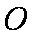
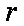
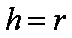
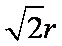
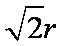

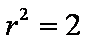
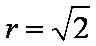
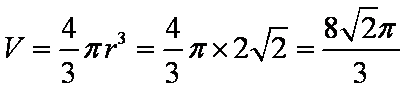
知识点
已知两个平面垂直,下列命题中:
①一个平面内已知直线必垂直于另一个平面内的任意一条直线;
②一个平面内已知直线必垂直于另一个平面内的无数条直线;
③一个平面内的任意一条直线必垂直于另一个平面;
④过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
其中正确命题的个数有
正确答案
解析
略
知识点
扫码查看完整答案与解析