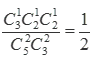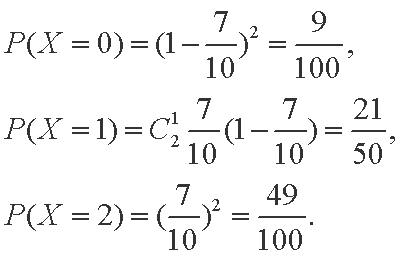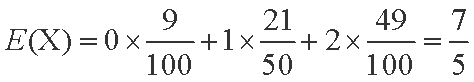- 计数原理的应用
- 共30题
用0,1,2,3,4排成无重复字的五位数,要求偶数字相邻,奇数字也相邻,则该五位数的个数是
正确答案
解析
排除法,偶数字相邻,奇数字也相邻有


知识点
甲、乙两人进行乒乓球比赛,先赢3局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次不同视为不同情形)共有( )
正确答案
解析
两人比赛局数为3局、4局或5局.当局数为3时,情况为甲或乙连赢3局,共2种;当局数为4时,若甲胜,则甲第4局胜,且前3局胜2局,有

知识点
某校学生会进行了一次关于“消防安全”的调查活动,组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查,活动结束后,团委会对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
表中所调查的居民年龄在[
(1)求上表中的m,n值,若从年龄在[20,30)的居民中随机选取两人,求这两人至少有一人知道灭火器使用方法的概率;
(2)在被调查的居民中,若从年龄在[10,20),[20,30)的居民中各随机选取2人参加消防知识讲座,记选中的4人中不知道灭火器使用方法的人数为

正确答案
见解析。
解析
(1)由题


记选取的两人至少有一人知道灭火器使用方法为事件A,
则
(2)随机变量
则



所以
所以

知识点
如果

正确答案
解析
二项展开式的通项为


知识点
甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,现做实验:从这两个箱子里各随机摸出2个球。求:
(1)摸出3个白球的概率;
(2)摸出至少两个白球的概率;
(3)若将摸出至少两个白球记为1分,否则记为0分,则一个人有放回地进行2次上述实验。求此人得分X的分布列及数学期望。
正确答案
见解析
解析
(1)设“在1次游戏中摸出i个白球”为事件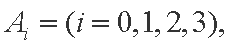
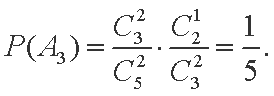
(2)设“至少两个白球”为事件B,则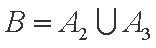
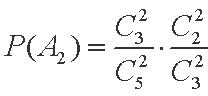
且A2,A3互斥,所以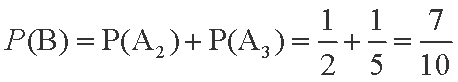
(3) X的所有可能取值为0,1,2.
所以X的分布列是
X的数学期望
知识点
扫码查看完整答案与解析