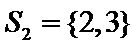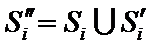- 集合的相等
- 共45题
1
题型:
单选题
|
1.已知集合


正确答案
C
解析
由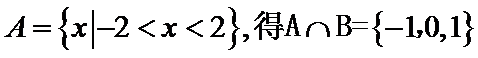
考查方向
集合交集
解题思路
1)要弄清构成集合的元素是什么(即元素的意义),是数集还是点集,
2)集合中的元素具有三性——确定性、互异性、无序性,特别是互异性,在判断集合中元素的个数时,以及在含参的集合运算中,常因忽视互异性,疏于检验而出错.
3)利用数轴来解使集合间的运算更简捷、直观.
易错点
容易忽视端点值
知识点
集合的相等
1
题型:
单选题
|
2.设集合

正确答案
C
解析



考查方向
本题考查集合的交集、指数函数的值域,二次不等式的解法,计算与求解能力,难度较低。
解题思路
结合函数性质及不等式解法求出集合A,B,然后求
易错点
数练掌握不等式的解法,求集合交集并集运算可结合数轴分析。
知识点
集合的相等
1
题型:
单选题
|
已知非零向量





正确答案
C
解析
略
知识点
集合的相等
1
题型:简答题
|
已知集合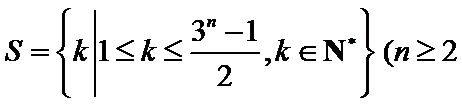

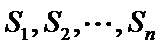


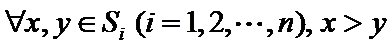



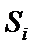



当




若集合
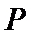


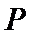

求证:

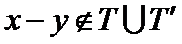
求证:对任意正整数


第(1)小题正确答案及相关解析
正确答案
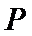

解析
当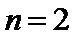

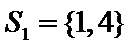

则


所以

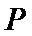
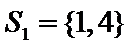

第(2)小题正确答案及相关解析
正确答案
证明详见解析
解析
①若

又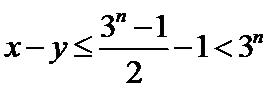


②若

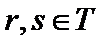
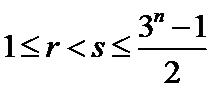
此时
所以

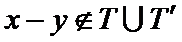
③若

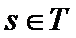
则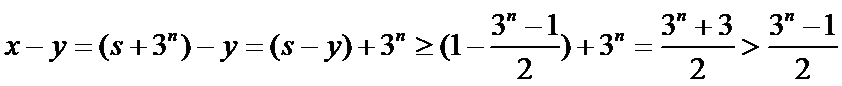
所以
又因为


所以
综上,对于


第(3)小题正确答案及相关解析
正确答案
证明详见解析
解析
假设


且


那么 当

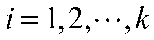
并构造如下

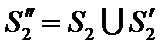


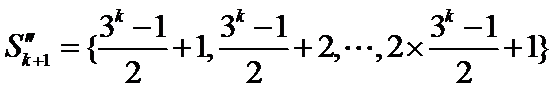
显然
又因为

下面证明


①若两个元素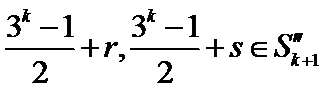

则
所以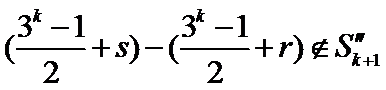
②若两个元素都属于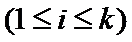
由(Ⅱ)可知,

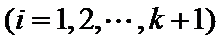
从而,
综上所述,对任意正整数

1
题型:
单选题
|
2.复数

正确答案
B
解析
略
知识点
集合的相等
下一知识点 : 并集及其运算
扫码查看完整答案与解析