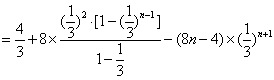- 等比数列
- 共373题
已知m是两个正数2和8的等比中项,则圆锥曲线

正确答案
解析
略
知识点
设Sn为数列{an}前n项和,对任意的n∈N*,都有Sn=2﹣an,数列{bn}满足
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)求数列{bn}的通项公式;
(3)求数列
正确答案
见解析。
解析
(1)当n=1时,a1=S1=2﹣a1,解得a1=1.
当n≥2时,an=Sn﹣Sn﹣1=an﹣1﹣an,即2an=an﹣1。
∴
∴数列{an}是首项为1,公比为

(2)b1=2a1=2. …(5分)
∵
∴

∴

∴
(3)∵
则
所以
即
则
②﹣①得
故
知识点
在如图所示的数阵中,第9行的第2个数为___________.
正确答案
66
解析
略
知识点
在等比数列


正确答案
84
解析
略
知识点
在等差数列

(1)求an与bn;
(2)设数列{Cn}满足cn=

正确答案
见解析。
解析
知识点
已知a>0,b>0,则
正确答案
解析
因为
当且仅当

故选C。
知识点
设数列








(1)求数列

(3)求满足

正确答案
见解析。
解析
(1)解:∵当

∴
∴
∵

∴
∴数列


∴
(2)解:由(1)得:
∴

(3)解:

令

故满足条件的最大正整数

知识点
已知数列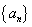
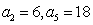
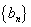
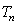
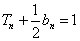
(1)求数列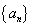
(2) 求证:数列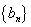
(3) 记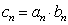
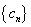
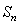
正确答案
见解析。
解析
(1)设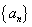
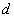
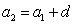
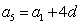
∵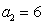
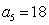
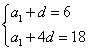
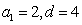
∴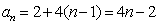
(2)当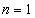
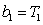
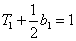
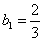
当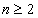
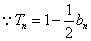
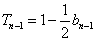
∴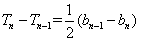
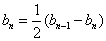
∴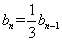
∴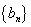
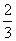
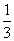
(3)由(2)可知: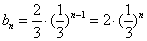
∴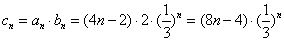
∴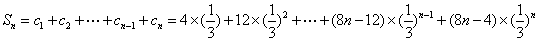
∴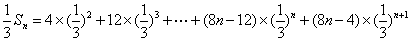
∴
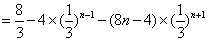
∴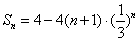
知识点
已知








(1)求数列

(2)将数列







正确答案
见解析。
解析
(1)

因为

所以

解得:


(2)由题知将数列





知识点
等比数列


(1)求
(2)数列



正确答案
见解析
解析
(1)



所以

(2)由(1)知
于是
假设存在正整数


整理得
解得
由

因此,存在正整数

知识点
扫码查看完整答案与解析