- 等比数列
- 共373题
在等差数列




正确答案
解析
由

知识点
已知








(1) 求证数列
(2)已知数列



(3)若数列



正确答案
见解析
解析
(1)∵
∴

∵

∴

又
∴数列

(2)依据(1)可以,得
于是,有

又

因此,数列

(3)由(2)可知,数列


故
因此,

将上述两个等式相减,得
可化简为
所以
知识点
已知数列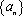
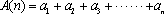
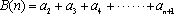
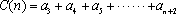
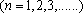
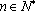
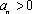
(1)若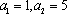
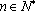
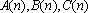
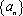
(2)证明:数列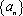
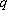
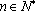
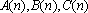
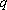
正确答案
见解析
解析
解析:(1)
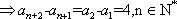
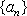
(2)(必
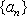
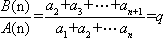
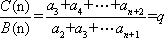
(充分性):若对于任意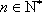
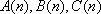
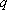
则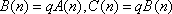
于是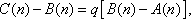
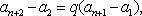
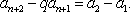
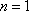
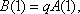
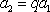
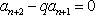
因为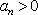
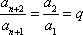

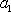
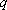
综上,数列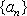
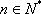

知识点
已知数列








(1)求数列

(2)令数列




正确答案
见解析。
解析
(1)由已知可知数列
∴数列

∵



又



(2)由已知得:
∴
∴
∴两式相减得

∴数列


知识点
已知数列


(1)若

(2)设





正确答案
见解析。
解析
(1)解法一:因为a3,a4,a5成等差数列,设公差为d,则a3=3-2d,a4=3-d。
因为a2,a3,a4成等比数列,所以
因为a2=1,所以


因为a1,a2,a3成等差数列,所以a1=2a2-a3=2-(3-2d)=
解法二:因为a1,a2,a3成等差数列,a2,a3,a4成等比数列,a3,a4,a5成等差数列,
则
则



解法三:因为a1,a2,a3成等差数列,则
因为a2,a3,a4成等比数列,则
因为a3,a4,a5成等差数列,则
解得:





(2)证法一:因为a2n-1,a2n,a2n+1成等差数列,a2n,a2n+1,a2n+2成等比数列,
所以2a2n=a2n-1+a2n+1,① a=a2na2n+2,②;所以a=a2n-2a2n,n≥2,③
由a1,a2及a2n-1,a2n,a2n+1是等差数列,a2n,a2n+1,a2n+2是等比数列,
可得a4=
所以
① 当n=2m,m
=-
② 当n=2m-1,m
=-
综上,对一切n∈N*,n≥2,有
证法二:①若n为奇数且n≥3时,则an,an+1,an+2成等差数列。
②若n为偶数且n≥2时,则an,an+1,an+2成等比数列,所以
由①②可知,对任意n≥2,n∈N*,
知识点
对大于或等于2的正整数的幂运算有如下分解方式:






根据上述分解规律,若


正确答案
11
解析
由








知识点
设等差数列




(1)求
(2)若从





①当

②若关于


正确答案
见解析。
解析
(1)设等差数列的公差为


所以
(2)因为数列


若




解得


若



另一方面,


所以对任何正整数




所以
(3)因为


所以当


当


而






下证当


则
因为


又因为



又因为当



综上所述,

知识点
已知数列
(1)试证数列

(2)在数列
(3)试证在数列


正确答案
见解析
解析
(1) 证明:由an+an+1=2n,得an+1=2n-an,
所以
又因为


所以an-


(2) 假设在数列{bn}中,存在连续三项bk-1,bk,bk+1(k∈N*, k≥2)成等差数列,则bk-1+bk+1=2bk,即[2k-1-(-1)k-1]+[2k+1-(-1)k+1]=2[2k-(-1)k],即2k-1=4(-1)k-1。
① 若k为偶数,则2k-1>0,4(-1)k-1=-4<0,所以,不存在偶数k,使得bk-1,bk,bk+1成等差数列,(7分)
② 若k为奇数,则当k≥3时,2k-1≥4,而4(-1)k-1=4,所以,当且仅当k=3时,bk-1,bk,bk+1成等差数列。
综上所述,在数列{bn}中,有且仅有连续三项b2,b3,b4成等差数列,(9分)
(3) 要使b1,br,bs成等差数列,只需b1+bs=2br,
即3+2s-(-1)s=2[2r-(-1)r],即2s-2r+1=(-1)s-2(-1)r-3,(﹡) (10分)
① 若s=r+1,在(﹡)式中,左端2s-2r+1=0,
右端(-1)s-2(-1)r-3=(-1)s+2(-1)s-3=3(-1)s-3,
要使(﹡)式成立,当且仅当s为偶数时,又s>r>1,且s,r为正整数,
所以当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列,(12分)
② 若s≥r+2时,在(﹡)式中,左端2s-2r+1≥2r+2-2r+1=2r+1,
由(2)可知,r≥3,所以r+1≥4,所以左端2s-2r+1≥16(当且仅当s为偶数、r为奇数时取“=”);右端(-1)s-2(-1)s-3≤0.所以当s≥r+2时,b1,br,bs不成等差数列,
综上所述,存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列。
知识点
等比数列



正确答案
解析
∵


知识点
Sn为等差数列{an}的前n项和,已知S5=5,S9=27,则S7= 。
正确答案
14
解析
∵数列{an}是等差数列,S5=5,S9=27,
∴
解得
∴S7=
知识点
扫码查看完整答案与解析