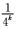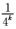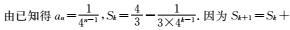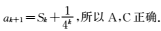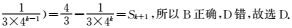等比数列_章节学习

1

题型：单选题

|

单选题 · 5 分

6.已知数列{an}是首项为1,公比为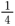的等比数列,且前n项和为Sn,则Sk+1与Sk的递推关系不满足（）

ASk+1=Sk+

BSk+1=1+Sk

CSk+1=Sk+ak+1

DSk+1=4Sk-3+ak+ak+1

正确答案

D

解析

知识点

等比数列的基本运算等比数列的性质及应用数列与不等式的综合

2

题型：单选题

|

单选题 · 5 分

6. 等比数列中，已知，则前5项和( )

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用

3

题型：单选题

|

单选题 · 5 分

8.已知等比数列{an},满足a1=,a3a5=4(a4-1)，则a2 = ( ）

A2

B1

C

D

正确答案

C

解析

a3a5=a42 =4（a4-1）,解得a4=2，所以q3=a4/a1=8,推出q=2.故a2=a1q=1/2,所以选C

考查方向

本题主要考查等比数列项数与项的概念和关系，属于中档题。

解题思路

利用所给条件求出公比q,进而求出等比数列的第2项。

易错点

对等比数列公比q 的理解错误

知识点

等比数列的基本运算等比数列的性质及应用

4

题型：填空题

|

填空题 · 5 分

13.Sn为等比数列{an}的前n项和，满足Sn=2an-1，则{an}的公比q= 。

正确答案

2

解析

当时，，解得；当时，，解得，所以{an}的公比q=。

考查方向

本题考查等比数列的基本性质，意在考查考生运算求解的能力。

解题思路

1.先令求出；

2. 令求出；

3.求出的值即为公比q.

易错点

不清楚前n项和与的关系；

知识点

由an与Sn的关系求通项an等比数列的基本运算

5

题型：简答题

|

简答题 · 12 分

17.在中，角的对边分别为，且， .

（Ⅰ）求角B的大小；

（Ⅱ）若等差数列的公差不为零，且=1，且成等比数列，求的前项和.

正确答案

（1）；

（2）.

解析

试题分析：本题第（1）问属于解三角形以及三角恒等变换的知识，是基础知识，难度中等；第（2）问是数列求和的问题，用主要考查了裂项相消法求数列的前n项和，解答过程如下：

【解】：（Ⅰ）由，所以，又，再由得

，即，，则为钝角。

，则，

解得。

（Ⅱ）设的公差为，由已知得，且.

∴ ．

又, ∴. ∴.

∴. ∴ .

考查方向

本题考查了解三角形以及数列的相关问题，主要考查了余弦定理、三角恒等变换、等差、等比数列的性质以及数列求和等知识，同时考查了转化化归思想以及运算求解能力。

解题思路

1、第（1）问根据余弦定理求出，然后再利用已知条件以及三角恒等变换公式进行转化求解即可。

2、第（2）问可以先用已知条件求出，然后利用裂项相消法求数列的前n项和。

易错点

本题容易因为忽略三角形内角的范围而导致错误的出现。

知识点

任意角的概念等比数列的基本运算

6

题型：单选题

|

单选题 · 5 分

7．已知等比数列{an}中，各项都是正数，且3a1，，2a2成等差数列，则等于（　　）

A6

B7

C8

D9

正确答案

D

解析

由3a1，，2a2等差可知，所以所以，即，解得，由等比数列{an}各项都是正数知q=3，所以，故选择D选项。

考查方向

本题主要考查了等比数列的性质,为高考必考题，在近几年的各省高考题出现的频率较高，常与数列的概念及性质等知识点交汇命题。

解题思路

先由3a1，，2a2等差求出公比q与首项a1的关系，进而求出的值。

易错点

等比数列相关性质不熟悉导致出错。

知识点

等比数列的基本运算

7

题型：单选题

|

单选题 · 5 分

8．若等比数列的各项均为正数，前4项的和为9，积为，则前4项倒数的和为（）

A

B

C1

D2

正确答案

D

解析

因为等比数列的各项均为正数，前4项的和为9，积为，

所以，设此等比数列的首项为a1 ，公比为q

前4项之和为S，前4项之积为P，前4项的倒数和为M

若q=1，则，此式无解

若，则

所以，

又因为前4项的和为9，积为，所以

所以答案选D

考查方向

本题主要考查了等比数列的有关知识，前n项和的公式运用等。

解题思路

1.对条件进行展开、变形；

2.设出前4项倒数的和M，对前4项的和与积这三个量进行转化，变形，整理从而得出结果。

A选项不正确， B选项不正确，C选项不正确，D选项正确。

易错点

本题给出两个条件，容易想到求出等比数列的基本量a1和q，但是在求解的时候就发现很不容易。

知识点

等比数列的基本运算等比数列的性质及应用

8

题型：单选题

|

单选题 · 5 分

12.已知数列满足，则（）

A

B

C

D

正确答案

C

解析

由知，而，所以，归纳可得，所以故，故选择C选项。

考查方向

本题主要考查了数列通项公式、数列求和等知识点,为高考必考题，在近几年的各省高考题出现的频率较高，常与数列的相关性质、数列求和等知识点交汇命题。

解题思路

由求数列的通项公式，再利用错位相减法求和。

易错点

不能求出的通项公式导致本题后面没法求和。

知识点

等比数列的基本运算

9

题型：填空题

|

填空题 · 5 分

14. 各项均为正数的等差数列中，，则前12项和的最小值为。

正确答案

72

解析

考查方向

本题主要考查了等差数列的性质和基本不等式。

解题思路

利用基本不等式得到第4项和第9项之和的最小值，然后利用等差数列的求和公式即可解出。

易错点

本题不知道联系基本不等式来解。

知识点

等比数列的基本运算

10

题型：单选题

|

单选题 · 5 分

5．已知等比数列满足，，则 ( )

A7

B15

C16

D53

正确答案

B

解析

先用等比数列性质求出a5=2,然后根据成公比为2的等比数列，再求和得15

考查方向

本题主要考查等比数列的性质和求和公式

解题思路

先用等比数列性质求出a5再用等比关系求和,

易错点

搞不清新等比数列的公比

知识点

等比数列的基本运算

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点