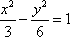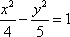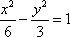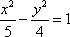双曲线的定义及标准方程
共311题

· 双曲线的定义及标准方程

双曲线的定义及标准方程
共311题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

双曲线的焦点到渐近线的距离为（）

正确答案

解析

略

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

已知双曲线的焦距为10 ，点在C的渐近线上，则C的方程为

正确答案

解析

设双曲线C ：-=1的半焦距为，则.

又C 的渐近线为，点P （2,1）在C 的渐近线上，，即.

又，，C的方程为-=1.

知识点

双曲线的定义及标准方程双曲线的几何性质

题型：简答题

简答题 · 12 分

如图，已知椭圆的离心率为，以该椭圆上的点和椭圆的左、右焦点为顶点的三角形的周长为.一等轴双曲线的顶点是该椭圆的焦点，设为该双曲线上异于顶点的任一点，直线和与椭圆的交点分别为和.

（1）求椭圆和双曲线的标准方程；

（2）设直线、的斜率分别为、，证明；

（3）是否存在常数，使得恒成立？若存在，求的值；若不存在，请说明理由。

正确答案

见解析。

解析

（1）设椭圆的半焦距为，由题意知，，又，

所以，，

又，因此。

故椭圆的标准方程为。

由题意设等轴双曲线的方程因为等轴双曲线的顶点是椭圆的焦点，所以

因此双曲线的标准方程为。

（2）设，

则，

因为点在双曲线上，所以。

因此，

即。

（3）由于的方程为，将其带入椭圆方程得

，

由根与系数的关系得

所以

。

同理可得。

则，

又，

所以。

故。

因此存在，使恒成立。

知识点

椭圆的定义及标准方程双曲线的定义及标准方程圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

题型：单选题

单选题 · 5 分

直线为双曲线的一条渐近线，则双曲线的离心率是（）

正确答案

A,B,C,D

解析

略

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

已知双曲线E的中心在原点，F（3，0）是E的焦点，过F的直线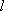与E相交于A，B两点，且AB的中点为N（－12，－15），则E的方程为（）

正确答案

解析

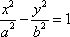
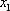
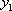
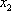
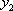
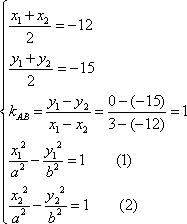
设双曲线E的方程为，A（，），B（，），则，

（1）－（2）得，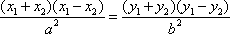

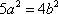
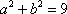
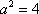
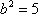
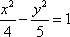
所以，又，解得，。因此双曲线E的方程为。

知识点

双曲线的定义及标准方程

继续学习学习下一知识点

下一知识点 : 双曲线的几何性质

百度题库 > 高考 > 理科数学 > 双曲线的定义及标准方程

扫码查看完整答案与解析