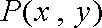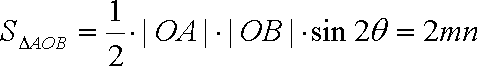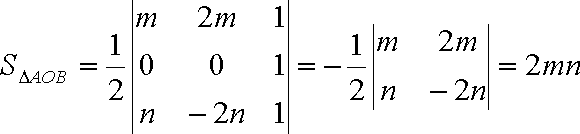- 双曲线的定义及标准方程
- 共311题
过双曲线的一个焦点的直线垂直于一条渐近线,且与双曲线的两支相交,则该双曲线离心率的取值范围是_________。
正确答案
解析
不妨设双曲线的方程为









知识点
已知双曲线
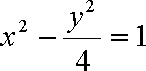
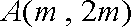
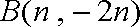
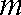
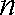


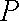
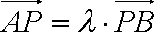
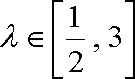
(1)用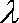
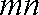
(2)求△

正确答案
见解析
解析
(1)由已知,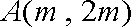
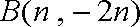


由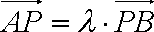
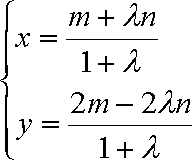
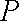
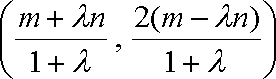
将
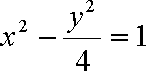
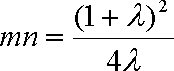
(2)解法一:设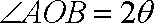
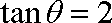
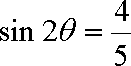
又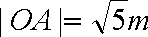
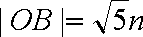
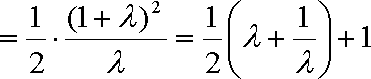
记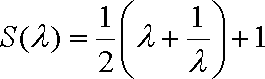
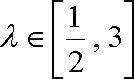
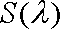
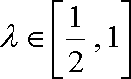
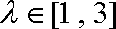
所以,当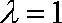
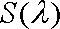
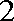
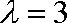
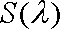

所以△
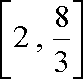
解法二:因为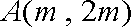
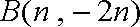


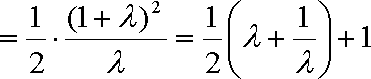
记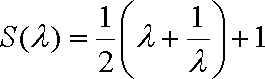
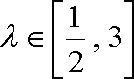
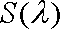
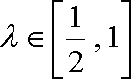
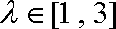
所以,当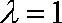
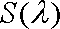
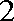
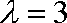
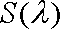

所以△
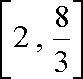
知识点
已知定点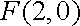
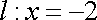


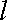
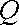
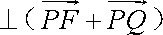


(1)求曲线
(2)过点
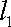

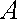
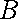
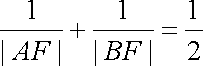
(3)记

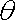

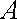
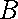
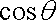
正确答案
见解析
解析
(1)设点
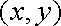
由题意,可得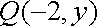
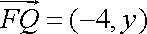
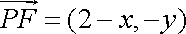
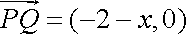
由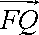
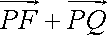
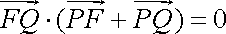
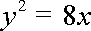

因此,所求曲线
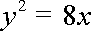

(2)因为过点

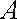
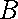
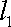
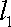
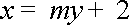
于是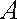
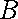
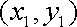
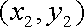
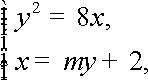
消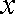
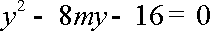
于是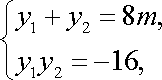
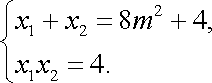
又因为曲线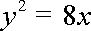

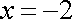
所以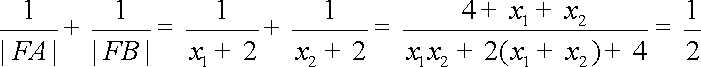
(3)由(2)可知,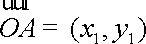
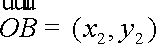
于是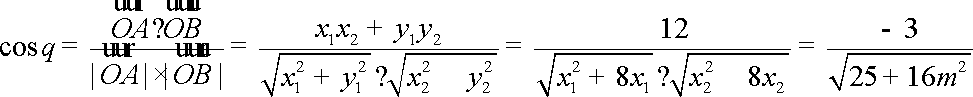
(16分)可求得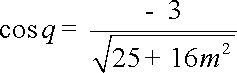
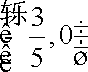
知识点
已知点








(1)求双曲线
(2)过圆






求证:
(3)过双曲线





正确答案
见解析
解析
(1)设

因为点




在



由双曲线的定义可知:
故双曲线

(2)①当切线
设

代入双曲线
所以
因为直线


设点

所以
即
②当切线
此时

(3)由条件可知:两条渐近线分别为
设双曲线

则点
所以
因为



故
设


所以
知识点
若双曲线

正确答案
解析
由双曲线








知识点
扫码查看完整答案与解析