- 函数模型的选择与应用
- 共46题
某厂以x千克/小时的速度匀速生产某种产品(生产条件要求

(1)要使生产该产品1小时获得的利润不低于1200元,求x的取值范围;
(2)要使生产120千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
正确答案
见解析
解析
知识点
某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件,该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为

(1)设生产A部件的人数为
(2)假设这三种部件的生产同时开工,试确定正整数
正确答案
见解析
解析
(1)设完成A,B,C三种部件的生产任务需要的时间(单位:天)分别为

期中
(2)完成订单任务的时间为




(i)当


由函数




故当

(ii)当






由函数



此时完成订单任务的最短时间大于
(iii)当





当


完成订单任务的最短时间为

综上所述,当
分别为44,88,68.
知识点
某工厂生产某种产品,每日的成本C(单位:元)与日产里x(单位:吨)满足函数关系式C=3+x,每日的销售额R(单位:元)与日产量x满足函数关系式
(1)求k的值;
(2)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
见解析。
解析
解:(1)由题意可得:L=
因为x=2时,L=3
所以3=2×2+
所以k=18
(2)当0<x<6时,L=2x+
所以L=2(x﹣8)+


当且仅当2(8﹣x)=
当x≥6时,L=11﹣x≤5
所以当x=5时,L取得最大值6
所以当日产量为5吨时,毎日的利润可以达到最大值6。
知识点
若函数h(x)满足
①h(0)=1,h(1)=0;
②对任意a∈[0,1],有h(h(a))=a;
③在(0,1)上单调递减。
则称h(x)为补函数,已知函数
(1)判断函数h(x)是否为补函数,并证明你的结论;
(2)若存在m∈[0,1],使h(m)=m,称m是函数h(x)的中介元,记


(3)当λ=0,x∈(0,1)时,函数y=h(x)的图像总在直线y=1-x的上方,求p的取值范围。
正确答案
见解析
解析
(1)函数h(x)是补函数,证明如下:
①

②对任意a∈[0,1],有
③令g(x)=(h(x))p,有
=
因为λ>-1,p>0,所以当x∈(0,1)时,g′(x)<0,
所以函数g(x)在(0,1)上单调递减,故函数h(x)在(0,1)上单调递减。
(2)当

(ⅰ)当λ=0时,中介元
(ⅱ)当λ>-1且λ≠0时,
由(*)得


综合(ⅰ)(ⅱ),对任意的λ>-1,中介元为

当n无限增大时,

故对任意的n∈N+,

(3)当λ=0时,

(ⅰ)当0<p≤1时,

所以点(xp,h(xp))不在直线y=1-x的上方,不符合条件;
(ⅱ)当p>1时,依题意只须
即xp+(1-x)p<1在x∈(0,1)时恒成立,
设φ(x)=xp+(1-x)p,x∈[0,1],
则φ′(x)=p[xp-1-(1-x)p-1],
由φ′(x)=0得


又因为φ(0)=φ(1)=1,所以当x∈(0,1)时,φ(x)<1恒成立。
综上,p的取值范围是(1,+∞)。
知识点
已知
正确答案
解析



知识点
某工厂生产某种产品,已知该产品的月生产量

正确答案
见解析。
解析
每月生产x吨时的利润为
由
得当 
∴
故
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
知识点
要测定古物的年代,常用碳的放射性同位素










(1) 求实数
(2) 测得湖南长沙马王堆汉墓女尸中
正确答案
(1)
(2)2100多年前
解析
(1)由题意可知,当


解得
(2)∵古墓中女尸
∴

解得
∴由此可推测古墓约是2100多年前的遗址。
知识点
某种商品每件进价12元,售价20元,每天可卖出48件,若售价降低,销售量可以增加,且售价降低

(1)试将该商品一天的销售利润表示成
(2)该商品售价为多少元时一天的销售利润最大?
正确答案
见解析
解析
(1)由题意可设,每天多卖出的件数为

又每件商品的利润为
∴该商品一天的销售利润为
(2)由
令

当


∴当商品售价为16元时,一天销售利润最大,最大值为432元
知识点
20. 某地区预计明年从年初开始的前x个月内,对某种商品的需求总量

(1)写出明年第x个月的需求量
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.甲、乙两公司同时开发同一种新产品,经测算,对于函数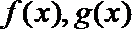
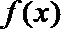
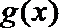
(1)试解释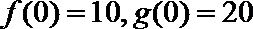
(2)设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析























