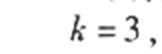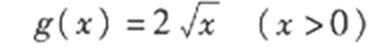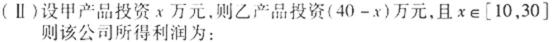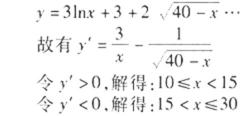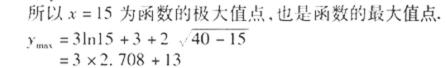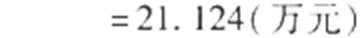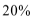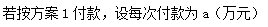- 函数模型的选择与应用
- 共46题
19.某工厂生产某种产品,每日的成本C(单位:元)与日产里



已知每日的利润


(Ⅰ)求
(Ⅱ)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
解:(Ⅰ)由题意可得:
解析
解析已在路上飞奔,马上就到!
知识点
20.某车间有50名工人,要完成150件产品的生产任务,每件产品由3个







(1)设完成




(2)为了在最短时间内完成全部生产任务,
正确答案
(1)生产150件产品,需加工A型零件450个,
则完成A型零件加工所需时间
生产150件产品,需加工
则完成
(2)设完成全部生产任务所需时间为



令


所以,当



故
当



则


当



则





解析
解析已在路上飞奔,马上就到!
知识点
21.有一种变压器铁芯的截面呈如图所示的正十字形,为保证所需的磁通量,要求正十字形的面积为4
正确答案
设外接圆半径为R,AB =x(0<x<R),DG =y,则4R2=x2+y2 (1),
由已知条件有2xy-x2=4

代入(1)得4R2= x2 +
∴4R2=

当且仅当
代入(2)得y=1+
∴当 x=2 且y=1+
此时正十字形外接圆周长最短。
答:正十字形的长和宽分别为(1+
解析
解析已在路上飞奔,马上就到!
知识点
19.请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得

(1)若广告商要求包装盒侧面积S(cm

(2)若广告商要求包装盒容积V(cm


正确答案
解:(1)由题意知, 包装盒的底面边长为







(2)包装盒容积V=

所以





所以当



解析
解析已在路上飞奔,马上就到!
知识点
20.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。(注:年利润一年销售收入一年总成本)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某公司研发甲、乙两种新产品,根据市场调查预测,甲产品的利润y(单位:万元)与投资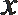
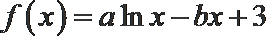
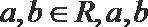
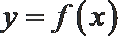
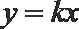
(I)分别求甲、乙两种产品的利润与投资资金间的函数关系式;
(II)已知该公司已筹集到40万元资金,并将全部投入甲、乙两种产品的研发,每种产品投资均不少于10万元.问怎样分配这40万元投资,才能使该公司获得最大利润?其最大利润约为多少万元?
(参考数据: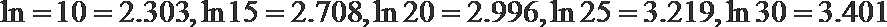
正确答案
所以:当甲产品投资15万元,
乙产品投资25万元时,
公司取得最大利润。
最大利润为21.124万元
解析
解析已在路上飞奔,马上就到!
知识点
21.政府决定用“对社会的有效贡献率”对企业进行评价用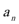
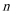
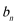

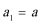
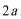
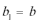
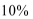

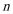
(1)求该企业第一年和第二年的“对社会的有效贡献率”;
(2)试问:从第几年起该企业“对社会的有效贡献率”不低于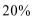
正确答案
(1)因为 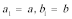
根据题意: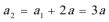

所以 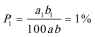

该企业第一年和第二年的“对社会的有效贡献率”分别为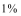
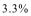
(2)因为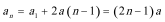
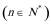
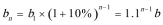
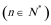
所以 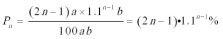
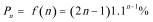
证法1: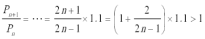
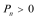
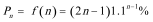
证法2: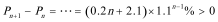

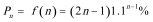
再验证: 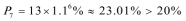
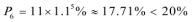
故,从第七年起该企业“对社会的有效贡献率”不低于
解析
解析已在路上飞奔,马上就到!
知识点
20.为了提高产品的年产量,某企业拟在2014年进行技术改革,经调查测算,产品当年的产量




(1)试确定


(2)该企业2014年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获利5万元,每吨乙产品可获
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某汽车销售公司为促销采取了较灵活的付款方式,对购买10万元一辆的轿车在一年内将款全部付清的前提下,可以选择以下两种分期付款方案购车:
方案1:分3次付清,购买后4个月第一次付款,再过4个月第二次付款,再过4个月第三次付款.
方案2:分12次付清,购买后1个月第一次付款,再过1个月第二次付款,……购买后12个月第十二次付款。
现规定分期付款中,每期付款额相同,月利率为0.8%,每月利息按复利计息,试比较以上两种方案的哪一种方案付款总数较少?(参考数据:1.0083=1.024,1.0084=1.033,1.00811=1.092,1.00812=1.1)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析