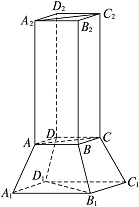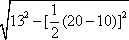- 直线和圆的方程的应用
- 共31题
如图,在平面直角坐标系


设圆


(1)若圆心



求切线的方程;
(2)若圆



标
正确答案
见解析
解析
(1)联立:
设切线为:
d=

故所求切线为:
(2)设点M(x,y),由

化简得:
即:点M的轨迹为以(0,1)为圆心,2为半径的圆,可记为圆D。
又因为点

故:1≤|CD|≤3,其中
解之得:0≤a≤
知识点
某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.
(1)证明:直线B1D1⊥平面ACC2A2;
(2)现需要对该零部件表面进行防腐处理,已知AB=10,A1B1=20,AA2=30,AA1=13(单位:厘米),每平方厘米的加工处理费为0.20元,需加工处理费多少元?
正确答案
见解析
解析
(1)因为四棱柱ABCD-A2B2C2D2的侧面是全等的矩形,
所以AA2⊥AB,AA2⊥AD。又因为AB∩AD=A,所以AA2⊥平面ABCD。
连接BD,因为BD⊂平面ABCD,所以AA2⊥BD。
因为底面ABCD是正方形,所以AC⊥BD。
根据棱台的定义可知,BD与B1D1共面
又已知平面ABCD∥平面A1B1C1D1,且平面BB1D1D∩平面ABCD=BD,
平面BB1D1D∩平面A1B1C1D1=B1D1,所以B1D1∥BD。于是
由AA2⊥BD,AC⊥BD,B1D1∥BD,可得AA2⊥B1D1,AC⊥B1D1.
又因为AA2∩AC=A,所以B1D1⊥平面ACC2A2.
(2)因为四棱柱ABCD-A2B2C2D2的底面是正方形,侧面是全等的矩形,所以S1=S四棱柱上底面+S四棱柱侧面=(A2B2)2+4AB·AA2=102+4×10×30=1 300(cm2)。
又因为四棱台A1B1C1D1-ABCD的上、下底面均是正方形,侧面是全等的等腰梯形,
所以S2=S四棱台下底面+S四棱台侧面
=(A1B1)2+4×
=202+4×
=1 120(cm2)。
于是该实心零部件的表面积为S=S1+S2=1 300+1 120=2 420(cm2),
故所需加工处理费为0.2S=0.2×2 420=484(元)
知识点
设集合
正确答案
解析


故答案为C
知识点
已知双曲线C:

(1)求a,b;
(2)设过F2的直线l与C的左、右两支分别交于A,B两点,且|AF1|=|BF1|,证明:|AF2|,|AB|,|BF2|成等比数列。
正确答案
见解析。
解析
(1)解:由题设知

所以C的方程为8x2-y2=8a2.
将y=2代入上式,并求得
由题设知,
所以a=1,
(2)证明:由(1)知,F1(-3,0),F2(3,0),C的方程为8x2-y2=8.①
由题意可设l的方程为y=k(x-3),
设A(x1,y1),B(x2,y2),则
x1≤-1,x2≥1,x1+x2=

于是|AF1|=
=
=-(3x1+1),
|BF1|=
=
=3x2+1.
由|AF1|=|BF1|得-(3x1+1)=3x2+1,
即x1+x2=
故
解得

由于|AF2|=
=
=1-3x1,
|BF2|=
=
=3x2-1,
故|AB|=|AF2|-|BF2|=2-3(x1+x2)=4,
|AF2|·|BF2|=3(x1+x2)-9x1x2-1=16.
因而|AF2|·|BF2|=|AB|2,所以|AF2|,|AB|,|BF2|成等比数列。
知识点
如图,在正方体





(1)求证:平面

(2)求证:

(3)设



正确答案
见解析
解析
(1)证明:在正方体
因为 



所以平面

(2)证明:连接



因为
所以 



又因为

所以 

所以 

即四边形
所以
又因为 



所以 

(3)解:满足条件
理由如下:
因为 

所以 
所以 
在正方体
因为 



所以 
又因为 
所以 
则点


所以在棱



同理,正方体


所以在正方体


知识点
函数
正确答案


解析
由
知识点
设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是( )
正确答案
解析
由题意画出图形如图:∵点M(x0,1),∴若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,
∴圆上的点到MN的距离的最大值为1,要使MN=1,才能使得∠OMN=45°,图中M′显然不满足题意, 当MN垂直x轴时,满足题意,∴x0的取值范围是[﹣1,1]。
知识点
下图为某算法的程序框图,则程序运行后输出的结果是__________。
正确答案
3
解析
当T=0,k=1时,
当T=1,k=2时,
当T=1,k=3时,
当T=1,k=4时,
当T=2,k=5时,
此时k≥6,所以输出T=3
知识点
已知圆

(1)求圆的标准方程;
(2)设点A为圆上一动点,AN

(3)在(2)的结论下,当


正确答案
解析
(1)设圆的半径为


所以,圆
(2)设动点



由题意,


将



(3)




设直线

联立方程
因为

又因为点








知识点
设函数




正确答案
[-1,+∞)
解析
如图作出函数






知识点
扫码查看完整答案与解析