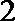- 直线和圆的方程的应用
- 共31题
8.若直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若复数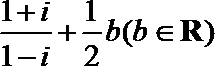
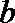
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知




(1)若直线



(2)对于线段








正确答案
见解析。
解析
(1)线段

线段

所以外接圆圆心

圆的方程为
设圆心




所以
当直线







综上,直线


(2)直线


因为点


又


所以
因为该关于




所以
又
所以

而
所以

又线段




故


知识点
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
正确答案
见解析。
解析
解法一:
(1)
如图,以O为坐标原点,OC所在直线为x轴,建立平面直角坐标系xOy.
由条件知A(0, 60),C(170, 0),
直线BC的斜率k BC=-tan∠BCO=-
又因为AB⊥BC,所以直线AB的斜率k AB=
设点B的坐标为(a,b),则k BC=
k AB=
解得a=80,b=120. 所以BC=
因此新桥BC的长是150 m.
(2)设保护区的边界圆M的半径为r m,OM=d m,(0≤d≤60)。
由条件知,直线BC的方程为
由于圆M与直线BC相切,故点M(0,d)到直线BC的距离是r,
即
因为O和A到圆M上任意一点的距离均不少于80 m,
所以

故当d=10时,
所以当OM = 10 m时,圆形保护区的面积最大.
解法二:
(1)
如图,延长OA, CB交于点F.
因为tan∠BCO=


因为OA=60,OC=170,所以OF=OC tan∠FCO=
CF=

因为OA⊥OC,所以cos∠AFB=sin∠FCO==
又因为AB⊥BC,所以BF=AF cos∠AFB==
因此新桥BC的长是150 m.
(2)设保护区的边界圆M与BC的切点为D,连接MD,则MD⊥BC,且MD是圆M的半
径,并设MD=r m,OM=d m(0≤d≤60)。
因为OA⊥OC,所以sin∠CFO =cos∠FCO,
故由(1)知,sin∠CFO =

因为O和A到圆M上任意一点的距离均不少于80 m,
所以

故当d=10时,
所以当OM = 10 m时,圆形保护区的面积最大.
知识点
执行如图所示程序框图,输出的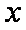
正确答案
解析
由程序框图可知: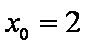
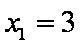
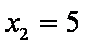
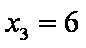
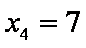
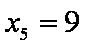
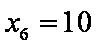
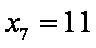
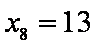
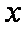
知识点
扫码查看完整答案与解析