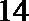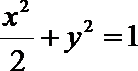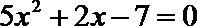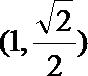- 直线和圆的方程的应用
- 共31题
12.已知x和y是正整数,且满足约束条件
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.过点C(2,5)且与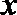
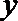
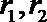
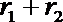
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知P为圆A:(x + l)2+y2=8上的动点,点B(1,0),线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为P.(1)求曲线P的方程;(2)当点P在第一象限,且COS∠BAP=
正确答案
1)圆A的圆心为A(-1,0),半径为
由已知得,
于是,
故曲线P是以A,B为焦点,
以
故曲线P的方程为
(2)由点P在第一象限,


于是直线AP方程为:
代入椭圆方程,消去y,可得,
所以,
由于点M在线段AP上,所以点M的坐标为
解析
已知圆心为A(-1,0),半径为

考查方向
本题主要考查直线和圆的方程的应用
解题思路
根据已知条件求出曲线的方程,根据曲线方程求出点的坐标。
易错点
椭圆的方程定义不清楚,计算能力弱
知识点
10.已知圆C:


正确答案
解析
如图,
设与直线






考查方向
解题思路
先要找到圆上哪一部分点到直线
易错点
本题容易因为不理解几何概型的角度模型而导致错误的产生。
知识点
20.已知P为圆A:(x + l)2+y2=8上的动点,点B(1,0),线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为P.
(1)求曲线P的方程;
(2)当点P在第一象限,且COS∠BAP=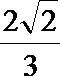
正确答案
(1)圆A的圆心为A(-1,0),半径为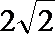
由已知得,
故曲线P是以A,B为焦点,
以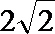
且
故曲线P的方程为
(2)由点P在第一象限,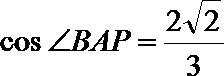
得
于是直线AP方程为:
消去y,可得,
所以,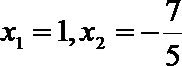
所以点M的坐标为
解析
已知圆心为A(-1,0),半径为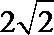
容易得到MA=MP,所以MA+MB=MA+MP,
故曲线P是以A,B为焦点,
以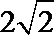
从而可求曲线方程,
当点P在第一象限,
求出点P的坐标,可得直线AP方程,
带入椭圆方程,消去y,即可得到M点的坐标。
考查方向
本题主要考查直线和圆的方程的应用
解题思路
根据已知条件求出曲线的方程,根据曲线方程求出点的坐标。
易错点
椭圆的方程定义不清楚,计算能力弱
知识点
扫码查看完整答案与解析