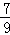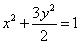三角函数的概念、同角三角函数的关系式和诱导公式
共1055题

三角函数的概念、同角三角函数的关系式和诱导公式
共1055题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：简答题

简答题 · 12 分

设的内角所对边的长分别是，且

（1）求的值；

（2）求的值.

正确答案

（1）a=2

（2）sin(A+)=.

解析

（1）由正弦定理知：.又b=3∴a=6cosB，又c=1，代入余弦定理，，得9=36os2B+1-12cos2B,解得cos2B=，又B为锐角，∴cosB=，∴a=2

（1）方法二：A=2B，得出，sinA=2sinBcosB,得出，b=3,c=1,代入得，a=

（2）由（1）知，cosA=2cos2B－1=－，∴sinA=,∴sin(A+)==.

知识点

任意角的概念

题型：单选题

单选题 · 5 分

设sin（+θ）=，则sin2θ=（　　）

A﹣

B﹣

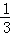
正确答案

解析

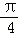
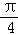
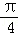
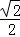
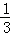
由sin（+θ）=sincosθ+cossinθ=（sinθ+cosθ）=，

两边平方得：1+2sinθcosθ=，即2sinθcosθ=﹣，

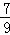
则sin2θ=2sinθcosθ=﹣。

故选A。

知识点

任意角的概念

题型：填空题

填空题 · 4 分

如图，△ABC中，AB=AC=2，BC=，点D 在BC边上，∠ADC=45°，则AD的长度等于______。

正确答案

解析

（法1）过A作AE⊥BC,垂足为E，∵AB=AC=2，BC=,∴E是BC的中点，且EC=，在中，AE==1,又∵∠ADE=45°，∴DE=1，∴AD=;

(法2) ∵AB=AC=2，BC=,由余弦定理知，

===, ∴C=30°，

在△ADC中，∠ADE=45°，由正弦定理得，，

∴AD===.

知识点

任意角的概念

题型：填空题

填空题 · 5 分

若将函数的图像向右平移个单位，所得图像关于轴对称，则的最小正值是___.

正确答案

解析

此题以三角函数图象的平移变换知识为背景，考察数形结合思想的运用意识。

知识点

任意角的概念

题型：填空题

填空题 · 5 分

设分别是椭圆的左、右焦点，过点的直线交椭圆于两点，若轴，则椭圆的方程为__________

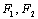
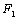
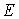
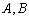
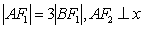
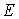
正确答案

解析

此题以椭圆知识运用为背景，考察数形结合思想、方程思想的运用意识，其中含有解题策略运用。

知识点

任意角的概念

题型：简答题

简答题 · 12 分

已知函数，其中

（1）当时，求在区间上的最大值与最小值；

(2)若，求的值.

正确答案

见解析。

解析

（1）当a=，θ=时，f（x）=sin（x+θ）+acos（x+2θ）

=sin（x+）+cos（x+）=sinx+cosx﹣sinx=﹣sinx+cosx

=sin（﹣x）=﹣sin（x﹣）。

∵x∈[0，π]，∴x﹣∈[﹣，]，

∴sin（x﹣）∈[﹣，1]，

∴﹣sin（x﹣）∈[﹣1，]，

故f（x）在区间[0，π]上的最小值为﹣1，最大值为。

（2）∵f（x）=sin（x+θ）+acos（x+2θ），a∈R，θ∈（﹣，），

f（）=0，f（π）=1，

∴cosθ﹣asin2θ=0 ①，﹣sinθ﹣acos2θ=1 ②，

由①求得sinθ=，由②可得cos2θ==﹣﹣。

再根据cos2θ=1﹣2sin2θ，可得﹣﹣=1﹣2×，

求得 a=﹣1，∴sinθ=﹣，θ=﹣。

综上可得，所求的a=﹣1，θ=﹣。

知识点

任意角的概念

题型：填空题

填空题 · 5 分

设是大于1的自然数，的展开式为.若点的位置如图所示，则

正确答案

解析

此题以二项式定理知识运用为背景，考察数形结合思想、方程思想的运用意识。

知识点

任意角的概念

题型：简答题

简答题 · 12 分

的内角A、B、C的对边分别为。已知，求C

正确答案

解析

由，得A为钝角且，

利用正弦定理，可变形为，

即有，

又A、B、C是的内角，故

或(舍去)

所以。

所以.

知识点

任意角的概念

题型：单选题

单选题 · 5 分

已知函数f(x)是定义在R上的奇函数，当x≥0时，.若,f(x-1)≤f(x),则实数a的取值范围为

A[]

B[]

C[]

D[]

正确答案

解析

当x≥0时，

f（x）=，

由f（x）=x﹣3a2，x＞2a2，得f（x）＞﹣a2；

当a2＜x＜2a2时，f（x）=﹣a2；

由f（x）=﹣x，0≤x≤a2，得f（x）≥﹣a2。

∴当x＞0时，。

∵函数f（x）为奇函数，

∴当x＜0时，。

∵对∀x∈R，都有f（x﹣1）≤f（x），

∴2a2﹣（﹣4a2）≤1，解得：。

故实数a的取值范围是。

知识点

集合的含义并集及其运算交集及其运算任意角的概念

继续学习学习下一知识点

下一知识点 : 三角函数的图象与性质

百度题库 > 高考 > 理科数学 > 三角函数的概念、同角三角函数的关系式和诱导公式

扫码查看完整答案与解析