- 直线与圆相交的性质
- 共47题
7.过三点A(1,3),B(4,2),C(1,7)的圆交于y轴于M、N两点,则
正确答案
知识点
14.已知M,N是圆


正确答案
解析
∵圆

圆
∴MN的方程为
∴
∴
考查方向
解题思路
先求出两圆的公共弦MN的方程,然后利用点B到直线MN的距离求出高BE,利用勾股定理求出MN即可
易错点
本题必须注意利用两圆相间得到公共弦方程
知识点
12.过点






正确答案
解析
有割线定理得,(PC-


设A(x,y),则(x+4)2+y2=10与圆
x=-1, y=


考查方向
解题思路
直线与圆相交的问题,常常考查求弦长问题,涉及到弦的中点即可使用圆的相关的几何性质,转化为直线垂直,进而求出斜率,使用点斜式求出方程。
易错点
1、本题点

2、两直线垂直的等价条件不能与直线的斜率联系起来。
知识点
19.如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
正确答案
当A,B两点离道路的交点都为2-
解析
解法一:如图,分别由两条道路所在直线建立直角坐标系xOy.
设A(a,0),B(0,b)(0<a<1,0<b<1),
则直线AB方程为
因为AB与圆C相切,所以
化简得 ab-2(a+b)+2=0,即ab=2(a+b)-2.
因此AB=
=
因为0<a<1,0<b<1,所以0<a+b<2,
于是AB=2-(a+b).
又ab=2(a+b)-2≤
解得0<a+b≤4-2

因为0<a+b<2,所以0<a+b≤4-2
所以AB=2-(a+b) ≥2-(4-2

当且仅当a=b=2-
所以AB最小值为2

答:当A,B两点离道路的交点都为2-
解法二:如图,连接CE,CA,CD,CB,CF.
设∠DCE=θ,θ∈(0,

在直角三角形CDA中,AD=tan
在直角三角形CDB中,BD=tan(

所以AB=AD+BD=tan


=tan

令t=tan
则AB=f(t)=t+


当且仅当t=
所以AB最小值为2
此时A,B两点离两条道路交点的距离是1-(

答:当A,B两点离道路的的交点都为2-
考查方向
解题思路
本题考查基本不等式在最值问题中的运用,解题步骤如下:
分别由两条道路所在直线建立直角坐标系xOy.设A(a,0),B(0,b)(0<a<1,0<b<1),求得直线AB的方程和圆的方程,运用直线和圆相切的条件:d=r,求得a,b的关系,再由两点的距离公式和基本不等式,解不等式可得AB的最小值,及此时A,B的位置.
易错点
读不懂题意,无法得出ab=2(a+b)-2,利用基本不等式求出最值
知识点


正确答案

解析
如图,


考查方向
解题思路
化为标准方程,
易错点
容易将方程的圆心坐标弄错,对图形的识别不准
知识点
正确答案
知识点
根据《票据法》的规定,下列有关票据背书的表述中,正确的有( )。
A.背书人在背书时记载“不得转让”字样的,被背书人再行背书无效
B.背书附条件的,背书无效
C.部分转让票据权利的背书无效
D.分别转让票据权利的背书无效
正确答案
C,D
解析
[解析] 根据《票据法》规定,背书时附有条件的,所附条件不具有汇票上的效力,但不影响背书行为本身的效力,被背书人仍可依该背书取得票据权利,故B项说法不正确。《票据法》还规定,背书人在汇票上记载“不得转让”字样,其后手再背书转让的,原背书人对后手的被背书人不承担保证责任,而原背书人只对直接的被背书人承担责任,故A项说法也不正确。
14.已知圆O:
正确答案
解析
设AC中点P(x,y)OP⊥AP,
AC=2PM,PM∈[

考查方向
解题思路
本题考查运用曲线的方程与几何图形知识解决问题的能力,先设AC中点P(x,y)OP⊥AP,AP=
AC=2PM,PM∈[

易错点
本题必须运用几何性质找曲线的方程,否则无从下手。
知识点
14.如图,圆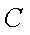
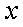
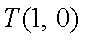
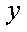
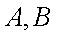
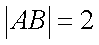
(1)圆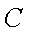
(2)过点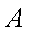
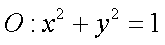
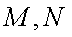
①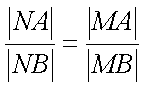
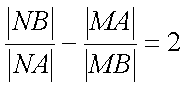
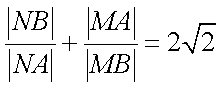
其中正确结论的序号是 _________. (写出所有正确结论的序号)
正确答案
(1)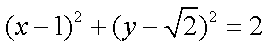
(2)①②③
解析
解析已在路上飞奔,马上就到!
知识点
7.过三点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析