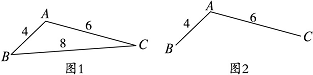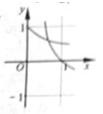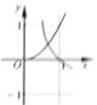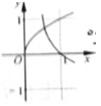- 指数函数的图像与性质
- 共51题
某地区规划道路建设，考虑道路铺设方案，方案设计图中，点表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小，例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10。
现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为__________。
正确答案
16
解析
由题意知，各城市相互到达，且费用最少为1＋2＋2＋3＋3＋5＝16＝FG＋GD＋AE＋EF＋GC＋BC
知识点
已知函数
A
B
C
D
正确答案
解析
由题可知
知识点
在同一直角坐标系中，函数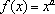
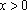
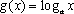
A
B
C
D
正确答案
解析
对A，没有幂函数的图象，；对B,
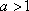
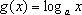
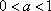
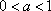
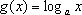
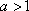
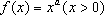
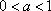
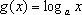
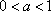
知识点
设函数
（1）判断函数
（2）设
（3）设函数
正确答案
见解析
解析
（1）函数
所以，
（2）
即
因为
所以，
所以，恒有
于是
（3）设函数
条件的不必要性的一个例子是。
此时
即
知识点
已知函数
A
B
C
D
正确答案
解析
略
知识点
电视传媒为了解某市100万观众对足球节目的收视情况，随机抽取了100名观众进行调查，如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图，将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”， 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”。
（1）试估算该市“足球迷”的人数，并指出其中“铁杆足球迷”约为多少人；
（2）该市要举办一场足球比赛，已知该市的足球场可容纳10万名观众，根据调查，如果票价定为100元/张，则非“足球迷”均不会到现场观看，而“足球迷”均愿意前往现场观看，如果票价提高
正确答案
（1）3万人（2）140元
解析
（1）样本中“足球迷”出现的频率=
“铁杆足球迷”=
所以16万“足球迷”中，“铁杆足球迷”约有3万人.
（2）设票价为
令
化简得：
解得：
即平均票价至少定为100+40=140元，才能使前往现场观看足球比赛的“足球迷”不超过10万人.
知识点
若
A
B
C
D
正确答案
解析
略。
知识点
已知
A
B
C
D
正确答案
解析
略
知识点
某品牌的汽车4S店，对最近100位采用分期付款的购车者进行统计，统计结果如下表所示：已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车，顾客分1期付款，其利润为1万元；分2期或3期付款共利润为1.5万元；分4期或5期付款，其利润为2万元.用
（1）求上表中的a，b值；
（2）若以频率作为概率，求事件A：“购买该器重汽车的3位顾客中，至多有1位采用3期付款”的概率P（A）；
（3）求
正确答案
见解析。
解析
（1）由
（2）记分期付款的期数为x，依题意得：
则“购买该品牌汽车的3位顾客中至多有1位采用3期付款”的概率:
（3）∵
∴
∴
知识点
若实数x,y满足条件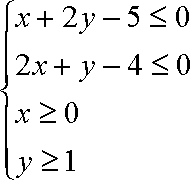
Azmax=0
Bzmax=
Czmin=
Dzmax =3
正确答案
解析
做出可行域，由图象可知当目标函数经过直线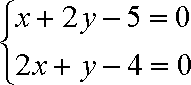
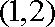
知识点
扫码查看完整答案与解析