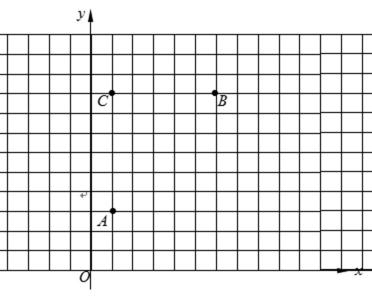
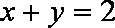奇函数
共21题

· 奇函数

奇函数
共21题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知函数，其中实数是常数。

（1）已知，，求事件：“”发生的概率；

（2）若是上的奇函数，是在区间上的最小值，求当时的解析式；

（3）记的导函数为，则当时，对任意，总存在使得，求实数的取值范围。

正确答案

见解析。

解析

（1）当时，等可能发生的基本事件共有9个：

其中事件： “”，包含6个基本事件：

故。即事件“”发生的概率

（2）是上的奇函数，得

∴ ,

① 当时，因为，所以，在区间上单调递减，

从而；

② 当时，因为，所以，在区间上单调递增，

从而,

综上，知

（3）当时，

当

，即

又，

而，

对任意，总存在使得

且，解得

知识点

奇函数

题型：单选题

单选题 · 5 分

函数（＞0，0＜＜）为偶函数，该函数的部分图象如图所示，A、B分别为最高点与最低点，并且，则该函数图象的一条对称轴方程为

正确答案

解析

略

知识点

奇函数

题型：单选题

单选题 · 5 分

设为定义在R上的奇函数，当时，，则

A－1

B－3

正确答案

解析

略

知识点

奇函数

题型：简答题

简答题 · 14 分

设, 为奇函数.

（1）求实数的值；

（2）设, 若不等式在区间上恒成立, 求实数的取值范围.

正确答案

见解析

解析

由f(x)是奇函数，可得a=1，所以，f（x）＝

（1）F（x）＝＋＝

由＝0，可得＝2，所以，x=1，即F（x）的零点为x＝1。

（2）f－1（x）＝，在区间上，由恒成立，即

≤恒成立，即恒成立

即，，所以，

知识点

奇函数

题型：简答题

简答题 · 16 分

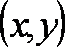
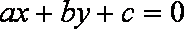
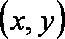
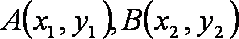
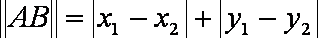
出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的。在出租车几何学中，点还是形如的有序实数对，直线还是满足的所有组成的图形，角度大小的定义也和原来一样。直角坐标系内任意两点定义它们之间的一种“距离”：，请解决以下问题：

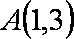
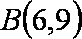
（1）求点、的“距离”；

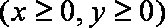
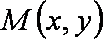
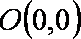
（2）求线段上一点的距离到原点的“距离”；

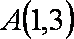
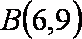
（3）定义:“圆”是所有到定点“距离”为定值的点组成的图形，点、，，求经过这三个点确定的一个“圆”的方程，并画出大致图像；（说明所给图形小正方形的单位是1）

正确答案

见解析

解析

（1） …………3分

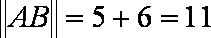
（2） …………6分

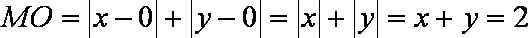
（3）设外心坐标，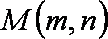

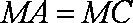
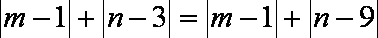
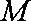
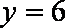
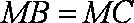
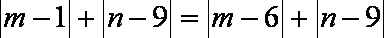
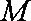
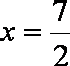
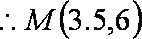
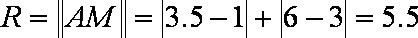
，，点在上…………7分

，，点在上…………8分

…………10分

…………14分

…………16分

知识点

奇函数

继续学习学习下一知识点

下一知识点 : 偶函数

百度题库 > 高考 > 文科数学 > 奇函数

扫码查看完整答案与解析