- 函数的周期性
- 共47题
14.若函数f(x)是定义R上的周期为2的奇函数,当0

正确答案
知识点
若函数f(x)是定义R上的周期为2的奇函数,当0

正确答案
-2
知识点
9.已知函数y=f(x)的周期为2,当x∈[-1,1]时,f(x)=x2,那么函数y=f(x)的图象与函数y=|lg x|的图象的交点共有 个。
正确答案
10
解析
在同一坐标系中作出函数y=f(x),y=|lg x|的图象如图,由图象可知,两个函数的图象的交点共有10个.
知识点
6.已知函数f(x)= 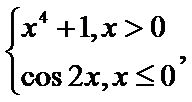
正确答案
解析
当x=1,f(1)=2,当x=-1,f(-1)=cos(-2)=cos2.所以A错。事实上,在不对称的区间上都是没有奇偶性的;
函数y=cos2x在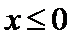
函数y=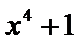
函数y=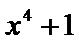
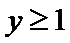
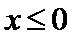
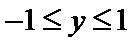
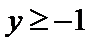
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1.对每一个选项进行判断即可;
2.也可以画出图像,直接判断。
A选项不正确, B选项不正确, C选项不正确,D选项正确。
易错点
1、本题不容易想到在x>0时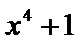
2、对于cos2x在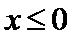
3、整个函数在定义域中的值域是求它们的交集容易出错。
知识点
12.已知偶函数






正确答案
解析
由










考查方向
本题主要考查了函数的性质(奇偶性、周期性)和方程的根的个数。
易错点
本题易在时由

知识点
扫码查看完整答案与解析


