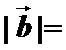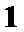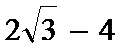- 平面向量的概念及线性运算、平面向量基本定理
- 共517题
8．已知
A
B
C
D
正确答案
解析
考查方向
解题思路
先根据垂直数量积为零求出未知参数m，再计算出b向量的模。
易错点
本题不知道向量垂直坐标满足的关系式。
知识点
4．已知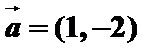
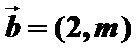
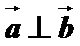
A
B
C
D
正确答案
解析
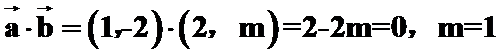
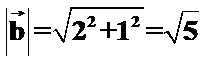
考查方向
解题思路
先根据垂直数量积为零求出未知参数m，再计算出b向量的模。
易错点
本题不知道向量垂直坐标满足的关系式 。
知识点
5. 已知不共线的两个向量
A
B2
C
D4
正确答案
解析
将已知的2个式子左右同时平方再相减即可得
【修改点】将已知
考查方向
解题思路
由垂直数量积为0得一个式子，由已知的模左右同时平方得一个式子，两式联立即可解出。
易错点
模的计算方法不清楚。
知识点
12．对
A
B
C
D
正确答案
解析
考查方向
解题思路
1）由向量可知
2）向量转化问题变为圆的方程
长度不超过6等价于
3）问题转化为两圆内切或内涵，进而求出n的范围
4）根据几何概型得出结果
易错点
主要易错于几何意义的构建
知识点
13．已知平面向量
正确答案
解析
分三种情况考虑：
（1）
（1）
（1）
三者比较大小后知应选
知识点
14．已知向量a=(1，
正确答案
2
解析
根据a=(1，
所以
即
考查方向
解题思路
本题考查平面向量的有关问题，
解题步骤如下：根据向量的坐标表示写出
易错点
1、向量模的求解出错；
2、向量的数量积的定义理解出错。
知识点
4．设
正确答案
解析
所以
考查方向
解题思路
由基本运算入手
易错点
考虑过多，想到向量的零向量，以及向量平行的同向和反向两种情况而误导出错
知识点
4．设向量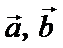
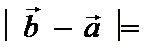
A1
B2
C-2
D
正确答案
解析
考查方向
解题思路
先使用向量减法的几何意义做
易错点
没理解向量模的 意义
知识点
3.平面向量
A
B0
C
D2
正确答案
解析
由
考查方向
本题主要考查了向量数量积的定义及数量积运算性质，在近几年的各省高考题出现的频率较高。
易错点
求模时忘记开方导致出错。
知识点
13．向量
正确答案
解析
由
考查方向
本题主要考查向量的相关知识。
解题思路
将垂直条件转化为数量积为0，代入数据求出
易错点
1.不能将垂直的条件进行转化。
2.夹角公式不清楚
知识点
扫码查看完整答案与解析