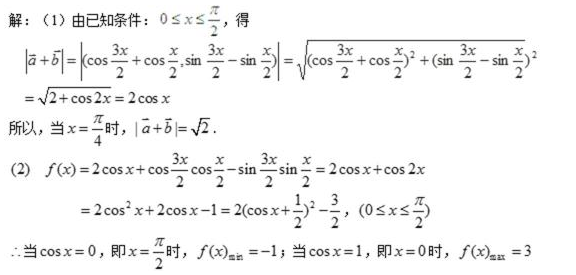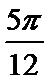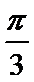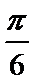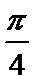- 平面向量的概念及线性运算、平面向量基本定理
- 共517题
11. 平面上


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知向量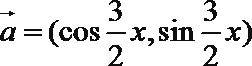
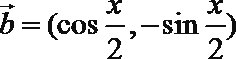
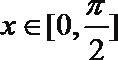
(1)当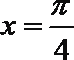
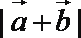
(2)设函数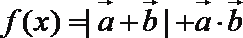
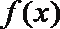
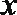
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若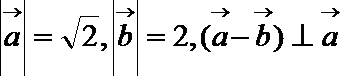
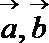
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知O.A.B是平面上的三点,向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知向量a,b,c满足

正确答案
解析
由
不妨设a=(2,0),b=(1,
由(a-c)·(b-2c)=0可得(2-x)(1-2x)+(-y)(
整理得2x2-5x+2y2-


则




知识点
5.已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是( )
正确答案
解析
因为(a-c)·(b-c)=0,所以(a-c)⊥(b-c).
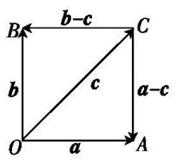
如图所示,设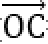
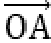
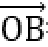
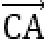
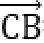
又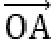
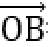
当且仅当OC为圆的直径时,|c|最大,且最大值为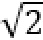
知识点
8.若a,b,c均为单位向量,且a·b=0,(a-c)·(b-c)≤0,则|a+b-c|的最大值为( )
正确答案
解析
设a=(1,0),b=(0,1),c=(x,y),则x2+y2=1,
a-c=(1-x,-y),b-c=(-x,1-y),
则(a-c)·(b-c)=(1-x)(-x)+(-y)(1-y)=x2+y2-x-y=1-x-y≤0,即x+y≥1,
又a+b-c=(1-x,1-y),
∴|a+b-c|=

∵c=(x,y)对应的点在

∴|a+b-c|的最大值为1.
知识点
21.已知向量a、b、c是同一平面内的三个向量,其中a=(1,2).
(1)若|c|=2
(2)若|b|=
正确答案
(1)令c=(x,y),则由|c|=2


又由a∥c知,2x-y=0②
联立①②可解得:

故c=(2,4)或c=(-2,-4).
(2)由a+2b与2a-b垂直知(a+2b)·(2a-b)=0,
即2a2+3a·b-2b2=0,∴a·b=
即|a||b|cosθ=

而由a=(1,2)知|a|=

∵θ∈[0,π],∴θ=π.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析