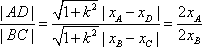- 点到直线的距离公式
- 共31题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在极坐标系中,点
正确答案
1
解析
在极坐标系中,点

知识点
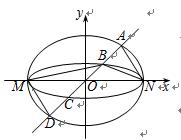
如图,已知椭圆
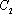

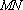

为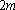
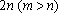

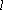
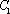
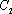
大到小依次为A,B,C,D,记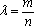
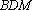
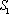
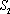
(1)当直线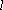
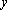
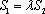
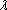
(2)当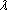
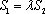
正确答案
(1)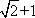

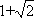
解析
依题意可设椭圆C1和C2的方程分别为
C1: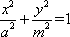
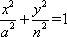
其中a>m>n>0,λ=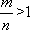
(1)解法1:
如图1,若直线l与y轴重合,即直线l的方程为x=0,则S1=



所以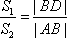
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=-m,
于是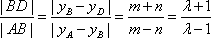
若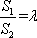
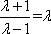
由λ>1,可解得λ=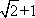
故当直线l与y轴重合时,若S1=λS2,则λ=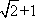
解法2:如图1,若直线l与y轴重合,则
|BD|=|OB|+|OD|=m+n,|AB|=|OA|-|OB|=m-n;
S1=

S2=

所以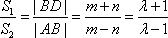
若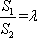
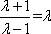
由λ>1,可解得λ=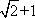
故当直线l与y轴重合时,若S1=λS2,则λ=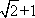
(2)解法1:
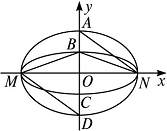
如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,则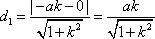
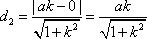
又S1=

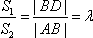
由对称性可知|AB|=|CD|,所以|BC|=|BD|-|AB|=(λ-1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是
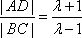
将l的方程分别与C1,C2的方程联立,可求得
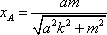
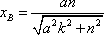
根据对称性可知xC=-xB,xD=-xA,于是
=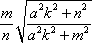
从而由①和②式可得
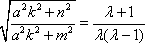
令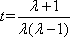
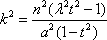
因为k≠0,所以k2>0.于是③式关于k有解,当且仅当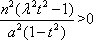
等价于

即
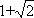
当1<λ≤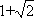
当λ>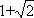
解法2:如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),
点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,
则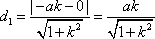
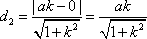
又S1=

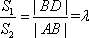
因为
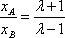
由点A(xA,kxA),B(xB,kxB)分别在C1,C2上,可得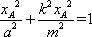
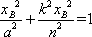
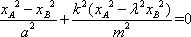
依题意xA>xB>0,所以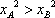
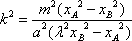
因为k2>0,所以由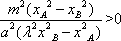
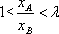
从而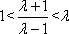
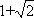
当1<λ≤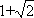
当λ>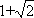
知识点
定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线C1:y=x 2+a到直线l:y=x的距离等于C2:x 2+(y+4) 2 =2到直线l:y=x的距离,
则实数a=______________。
正确答案
解析
C2:x 2+(y+4) 2 =2,圆心(0,—4),圆心到直线l:y=x的距离为:

另一方面:曲线C1:y=x 2+a,令




知识点
扫码查看完整答案与解析