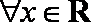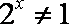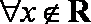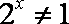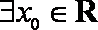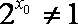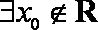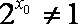- 命题及其关系、充分条件与必要条件
- 共805题
下列各命题中正确的命题是
① “若a, b都是奇数,则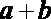
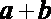
② 命题“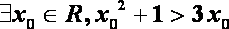
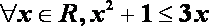
③ “函数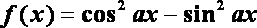
④“平面向量
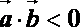
正确答案
解析
若a, b都是奇数,则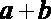
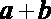
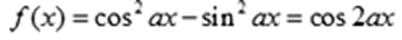
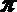
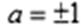
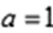
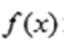
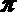
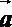
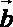
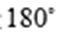
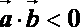
知识点
“




正确答案
1
解析
若





知识点
已知

①若

②若

③若

④若

其中真命题是
正确答案
②④
解析
①:只有当




知识点
已知


正确答案
解析




但是




知识点
若a、b、c是常数,则“a>0且b2﹣4ac<0”是“对任意x∈R,有ax2+bx+c>0”的( )
正确答案
解析
解:若a>0且b2﹣4ac<0,则对任意x∈R,有ax2+bx+c>0,
反之,则不一定成立,如a=0,b=0且c>0时,也有对任意x∈R,有ax2+bx+c>0。
故“a>0且b2﹣4ac<0”是“对任意x∈R,有ax2+bx+c>0”的充分不必要条件
知识点
已知命题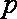
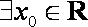
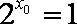
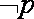
正确答案
解析
特称命题的否定是全称命题,故选A。
知识点
设

给定下列四个命题,其中为真命题的序号是___▲__。
①

③
正确答案
②③
解析
①错误,m与
知识点
已知命题p:对m∈[-1,1],不等式a2-5a-3≥


正确答案
解析
解析:∵m∈[-1,1],
∴

∵对m∈[-1,1],不等式a2-5a-3≥
故命题p为真命题时,a≥6或a≤-1.
又命题q:不等式x2+ax+2<0有解,
∴Δ=a2-8>0,∴a>2

从而命题q为假命题时,-2

∴命题p为真命题,q为假命题时,a的取值范

知识点
“

正确答案
解析
若直线


知识点
已知条件



正确答案
解析


知识点
扫码查看完整答案与解析