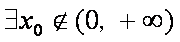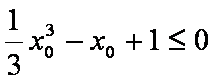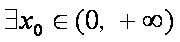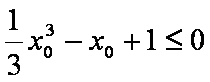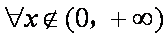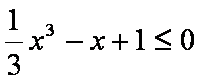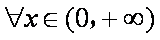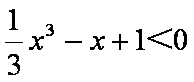命题及其关系、充分条件与必要条件
共805题

命题及其关系、充分条件与必要条件
共805题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

命题“若，则”的否命题是

A若，则

B若，则

C若，则

D若，则

正确答案

解析

略

知识点

四种命题及真假判断

题型：填空题

填空题 · 5 分

对于两个图形F1，F2，我们将图形F1上的任意一点与图形F2上的任意一点间的距离中的最小值，叫作图形F1与图形F2的距离，若两个函数图象的距离小于1，称这两个函数互为“可及函数”，给出下列几对函数，其中互为“可及函数”的是　　，（写出所有正确命题的编号）

①f（x）=cosx，g（x）=2；

②f（x）=ex，g（x）=x；

③f（x）=log2（x2﹣2x+5），g（x）=sinx；

④f（x）=x+，g（x）=lnx+2；

⑤f（x）=，g（x）=x+。

正确答案

②④

解析

①f（x）=cosx的最低点与g（x）=2的距离等于1，故不满足题意；

②f（x）=ex，则f′（x）=ex，设切点为（a，ea），则ea=1，∴a=0，∴切点为（（0，1），切线方程为y=x+1，则与g（x）=x的距离为＜1，满足题意；

③f（x）=log2（x2﹣2x+5）≥2，g（x）=sinx≤1，∴两个函数图象的距离大于等于1，不满足题意；

④x=时，f（x）=x+=2，g（x）=lnx+2=ln+2，两个函数图象的距离小于1，满足题意；

⑤f（x）=表示以原点为圆心，2为半径的上半圆，圆心到g（x）=x+的距离为=3，∴两个函数图象的距离最小值为1，不满足题意。

故答案为：②④。

知识点

四种命题及真假判断

题型：单选题

单选题 · 5 分

命题“，”的否定是（）

A.，

B.，

C.，

D.，

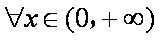
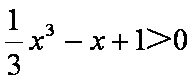
正确答案

解析

略

知识点

四种命题及真假判断

题型：填空题

填空题 · 5 分

有下列命题：

①已知a，b是平面内两个非零向量，则平面内任一向量都可表示为，其中λ，μ∈R；

②对任意平面四边形ABCD，点E、F分别为AB、CD的中点，则；

③直线x﹣y﹣2=0的一个方向向量为（1，﹣1）；

④已知a与b夹角为，且•=，则|﹣|的最小值为；

⑤是（a•b）•c=a•（b•c）的充分条件；

其中正确的是　　（写出所有正确命题的编号）。

正确答案

②④⑤

解析

当与是共线向量时，根据平面向量基本定理可得①不正确。

对任意平面四边形ABCD，点E、F分别为AB、CD的中点，∴=，=；

再根据 =，=，相加可得，故②正确。

直线x﹣y﹣2=0的一个方向向量为（1，1），故③不正确。

已知与夹角为，且•=，则||•||•cos=||•||=2，

|a﹣b|==≥==﹣1，

故|a﹣b|的最小值为，故④正确。

若，则=λ，可得（a•b）•c=||•||•cos＜，＞•λ，

a•（b•c）=||•||•cos＜，＞λ||=||•||•cos＜，＞•λ，

∴（a• b）•c=a•（b•c），

∴是（a•b）•c=a•（b•c）的充分条件，故⑤正确。

知识点

四种命题及真假判断

题型：单选题

单选题 · 5 分

以下有四种说法：

①若p或q为真，p且q为假，则p与q必为一真一假；

②若数列的前n项和为Sn=n2+n+l，n∈N*，则∈N*

③若实数t满足，则称t是函数f（x）的一个次不动点，设函数f（x）=Inx与函数g（x）=ex（其中e为自然对数的底数）的所有次不动点之和为m，则m=0

④若定义在R上的函数f（x）满足，则6为函数f（x）的周期

以上四种说法，其中说法正确的是

A①③

B③④

C①②③

D①③④

正确答案

解析

①若p或q为真，p且q为假，则p与q必为一真一假，正确；

②若数列，错误。；

③若实数t满足的一个次不动点，设函数与函数为自然对数的底数）的所有次不动点之和为m，则m=0，正确。由函数的性质知：方程和方程的两个互为相反数，所以此命题正确；

④若定义在R上的函数则6是函数的周期，正确。因为，所以，所以周期为6.

知识点

四种命题及真假判断

题型：单选题

单选题 · 5 分

若集合A={1，m，m2}，集合B一{2，4}，则“m=－2”是“AB={4}”的

A充分不必要条件

B必要不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

略

知识点

四种命题及真假判断

题型：填空题

填空题 · 5 分

命题P：对∀x≥0，都有x3﹣1≥0，则￢p是　，使得x3﹣1＜0　。

正确答案

∃x≥0

解析

根据全称命题的否定是特称命题即可得到：

￢p：∃x＜0，使得x3﹣1＜0，

故答案为：∃x≥0，使得x3﹣1＜0

知识点

四种命题及真假判断

题型：单选题

单选题 · 5 分

若命题为假命题，则

A、中至少有一个为真命题

B、中至多有一个为真命题

C、均为真命题

D、均为假命题

正确答案

解析

易知为真，故选A.

知识点

四种命题及真假判断

题型：单选题

单选题 · 5 分

“成等差数列”是“”成立的（）

A充分非必要条件

B必要非充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

当x,z都取负数时. 无意义。选A.

知识点

四种命题及真假判断

题型：简答题

简答题 · 14 分

已知集合，集合，集合.

命题，命题

（1）若命题为假命题，求实数的取值范围；

（2）若命题为真命题，求实数的取值范围。

正确答案

见解析

解析

（1）由命题是假命题，可得，即得.

（2）为真命题，都为真命题，

即且

有，

解得.

知识点

四种命题及真假判断

继续学习学习下一知识点

下一知识点 : 简单的逻辑联结词、全称量词与存在量词

百度题库 > 高考 > 文科数学 > 命题及其关系、充分条件与必要条件

扫码查看完整答案与解析