- 向量的加法及其几何意义
- 共71题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
集合{－1,0,1}共有__________个子集。
正确答案
8
解析
由于集合{－1,0,1}有3个元素，故其子集个数为23＝8.
知识点
若向量
A
B
C
D
正确答案
解析
略
知识点
在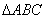
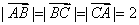
A
B
C
D
正确答案
解析
知识点
如图，正六边形ABCDEF中，
A
B
C
D
正确答案
解析
知识点
执行如图3所示的程序框图，如果输入
正确答案
9
解析
略
知识点
已知双曲线
（1）求实数
（
（3）若点
正确答案
见解析。
解析
（1）解：设双曲线
由题意可得
解得
（2）证明：由（1）可知，直线
因为
所以
因为点
所以
所以直线
（3）证法1：设点
设
即
整理，得
由①×③，②×④得
将
得
将⑤代入⑦，得
所以点
证法2：依题意，直线
设直线
由
消去
因为直线
则有
设点
由
整理得
将②③代入上式得
整理得
因为点
联立④⑤消去
所以点
知识点
如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，那么m＋n＝( )。
正确答案
解析
由CE与AB共面，且与正方体的上底面平行，则与CE相交的平面个数m＝4.作FO⊥底面CED，一定有面EOF平行于正方体的左、右侧面，即FE平行于正方体的左、右侧面，所以n＝4，m＋n＝8.故选A
知识点
已知变量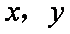
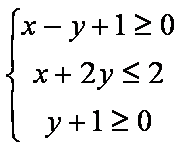
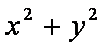
正确答案
17
解析
由题设可得，点（0，0）在可行域内，故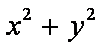
时，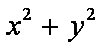
知识点
扫码查看完整答案与解析