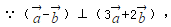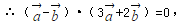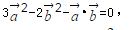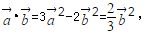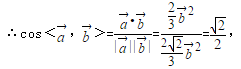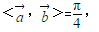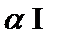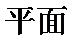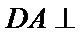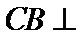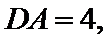- 向量的加法及其几何意义
- 共71题
13．已知点
正确答案
外心、重心、垂心
解析
解析已在路上飞奔，马上就到！
知识点
7. 在
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．如图，在三棱锥
（1）求证：平面
（2）当角
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14． 已知
正确答案
解析
如图所示，设
由三角形外接圆的性质可得
∴
∵
两边与
∴
由正弦定理可得
化简得
又∵
∴
又∵
∴
∴
考查方向
本题综合考查了三角形外接圆的性质、垂径定理、正弦定理、数量积运算性质、两角和差的余弦公式、三角函数基本关系式等基础知识与基本技能方法，考查了分析问题和解决问题的能力，属于难题．这类问题在近几年各省市的高考试卷中出现频率很高，以平面向量为载体，可以与三角、函数、数列、解析几何等知识结合交汇命题．
解题思路
取
由向量的三角形法则可得
易错点
对条件
知识点
3.设
A
B
C
D
正确答案
解析
由题知“（）是
∵
∴
考查方向
本题主要考查空间线面位置关系的表示及线面位置关系的判定和性质，还考查了逻辑关系中充要关系的判断,在近几年的各省高考题出现的频率较高，多与各部分知识交汇命题为主，较易。
解题思路
理解清“充分条件是”是倒装形式，建议改为“（）是
易错点
本题易在“充分条件是”的“是”字的理解上出错。
知识点
6．若非零向量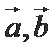
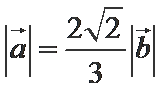
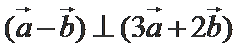
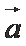
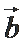
A
B.
C
D
正确答案
解析
解：
即：
即：
即：
故选：D.
考查方向
数量积表示两个向量的夹角．
解题思路
根据向量垂直的等价条件以及向量数量积的应用进行求解即可．
易错点
由向量垂直的等价条件计算向量的数量积，容易出错.
教师点评
本题主要考查向量夹角的求解，利用向量数量积的应用以及向量垂直的等价条件是解决本题的关键．
知识点
7.在平面直角坐标系中，若不等式组
A
B
C
D
正确答案
解析
由题可知，A(2,2a+1),B(1,a+1), 
所以
考查方向
解题思路
建立适当的坐标系，利用线性规划理论，根据区域的面积求参数的值
知识点
7.在梯形
A
B
C
D
正确答案
解析
在梯形
考查方向
解题思路
在梯形
易错点
在平面几何图形中向量的加法运算掌握不好。
知识点
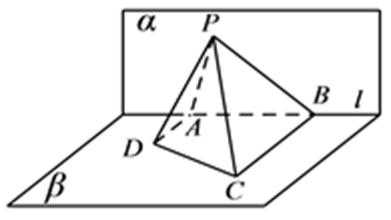
8.如图，已知平面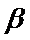
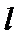
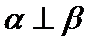
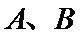
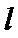
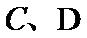
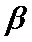
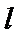
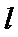
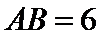
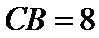
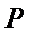
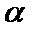
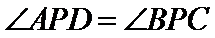
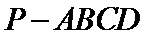
A48
B
C
D
正确答案
解析
由题意知：三角形PAD，三角形PBC是直角三角形，有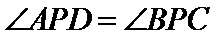
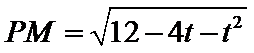
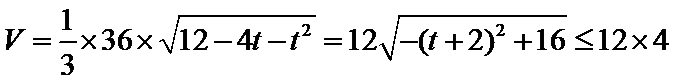
考查方向
解题思路
先根据已知条件，用参数表示四棱锥的体积，然后找到最大值的情况。
易错点
判断最大值时的情况
知识点
扫码查看完整答案与解析