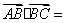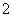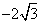- 向量的加法及其几何意义
- 共71题
1
题型:填空题
|
集合{-1,0,1}共有__________个子集。
正确答案
8
解析
由于集合{-1,0,1}有3个元素,故其子集个数为23=8.
知识点
向量的加法及其几何意义
1
题型:
单选题
|
若向量


正确答案
A
解析
略
知识点
向量的加法及其几何意义
1
题型:
单选题
|
在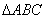
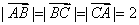
正确答案
B
解析
知识点
向量的加法及其几何意义
1
题型:简答题
|
已知双曲线










(1)求实数
(


(3)若点










正确答案
见解析。
解析
(1)解:设双曲线

由题意可得
解得
(2)证明:由(1)可知,直线



因为

所以
因为点



所以

所以直线


(3)证法1:设点









设

即
整理,得
由①×③,②×④得
将

得
将⑤代入⑦,得
所以点

证法2:依题意,直线

设直线

由
消去

因为直线



则有
设点
由

整理得
将②③代入上式得
整理得
因为点


联立④⑤消去

所以点

知识点
向量的加法及其几何意义
1
题型:填空题
|
已知变量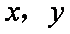
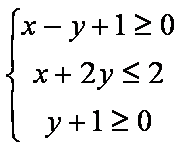
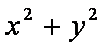
正确答案
17
解析
由题设可得,点(0,0)在可行域内,故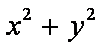
时,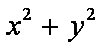
知识点
向量的加法及其几何意义
下一知识点 : 向量的减法及其几何意义
扫码查看完整答案与解析