- 概率与统计
- 共1631题
18. 已知

(Ⅰ)如果该同学10所高校的考试都参加,试求恰有2所通过的概率;
(Ⅱ)假设该同学参加每所高校考试所需的费用均为


正确答案
(Ⅰ)因为该同学通过各校考试的概率均为

(Ⅱ)设该同学共参加了


∵
∴所以该同学参加考试所需费用
所以
令
则
由(1)-(2)得
所以
所以

解析
解析已在路上飞奔,马上就到!
知识点
17.某次数学测验共有8道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对l道题得5分,不选或选错得0分.某考生每道题都选并能确定其中有6道题能选对,其余2道题无法确定正确选项,但这2道题中有1道题能排除两个错误选项,另1道只能排除一个错误选项,于是该生做这2道题时每道题都从不能排除的选项中随机选一个选项作答,且各题作答互不影响.
(1)求该考生本次测验选择题得40分的概率;
(2)求该考生本次测验选择题所得分数的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.一个盒子装有六张卡片,上面分别写着如下六个函数:





(Ⅰ)从中任意拿取
(Ⅱ)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
正确答案
(Ⅰ)





所有的基本事件包括两类:一类为两张卡片上写的函数均为奇函数;
另一类为两张卡片上写的函数为一个是奇函数,
一个为偶函数;故基本事件总数为
满足条件的基本事件为两张卡片上写的函数均为奇函数,故满足条件的基本事件个数为
故所求概率为
(Ⅱ)


故


解析
解析已在路上飞奔,马上就到!
知识点
18.某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.(某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了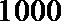
(1)完成列联表,并判断能否有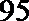
(参考数据与公式: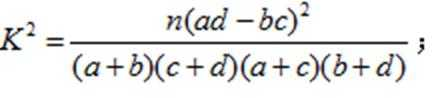
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
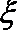

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某中学有6名爱好篮球的高三男生,现在考察他们的投篮水平与打球年限的关系,每人罚篮10次,其打球年限与投中球数如下表:
(Ⅰ)求投中球数

(Ⅱ)现在从高三年级大量男生中调查出打球年限超过



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某种家用电器每台的销售利润与该电器的无故障时间T(单位:年)有关,若T







(Ⅰ)求
(Ⅱ)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某工厂2011年第一季度生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品,参加四月份的一个展销会.

(1)问A,B,C,D型号的产品各抽取多少件?从50件样品中随机的抽取2件,求这两件产品恰好是不同型号的产品的概率;
(2)从A,C型号的产品中随机的抽取3件,用ξ表示抽取A种型号的产品件数,求ξ的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域














(Ⅰ)小明的两次回球的落点中恰有一次的落点在乙上的概率;
(Ⅱ)两次回球结束后,小明得分之和
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ.求ξ的分布列及数学期望E(ξ).(结果用最简分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.有一批产品,其中有




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析