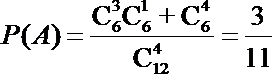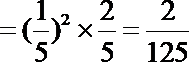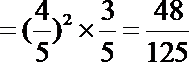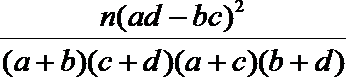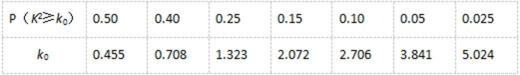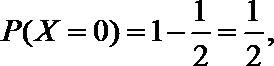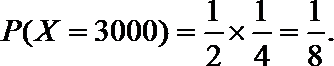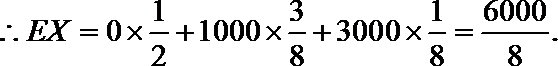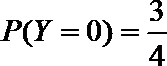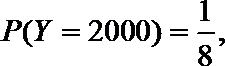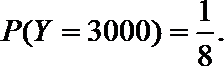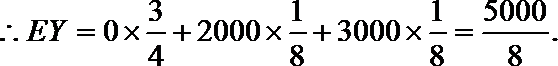- 概率与统计
- 共1631题
19. 二十世纪50年代,日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状,人们把它称为水俣病。经调查发现一家工厂排出的废水中含有甲基汞,使鱼类受到污染.人们长期食用含高浓度甲基汞的鱼类引起汞中毒,引起世人对食品安全的关注。《中华人民共和国环境保护法》规定食品的汞含量不得超过1.00ppm.
罗非鱼是体型较大,生命周期长的食肉鱼,其体内汞含量比其他鱼偏高.现从一批罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前一位数字为茎,小数点后一位数字为叶)如下:
(Ⅰ)若某检查人员从这15条鱼中,随机地抽出3条,求恰有1条鱼汞含量超标的概率;
(Ⅱ)以此15条鱼的样本数据来估计这批鱼的总体数据。若从这批数量很大的鱼中任选3条鱼,记ξ表示抽到的鱼汞含量超标的条数,求ξ的分布列及Eξ。
正确答案
(I)记“15条鱼中任选3条恰好有1条鱼汞含量超标”为事件A
则
∴15条鱼中任选3条恰好有1条鱼汞含量超标的概率为
(II)解法一:依题意可知,这批罗非鱼中汞含量超标的鱼的概率P=
所有ξ的取值为0,1,2,3,其分布列如下:
所以ξ~
所以Eξ=1.
解法二:依题意可知,这批罗非鱼中汞含量超标的鱼的概率P=
所有ξ的取值为0,1,2,3,其分布列如下:
所以Eξ=
解析
解析已在路上飞奔,马上就到!
知识点
19.英语老师要求学生从星期一到星期四每天学习3个英语单词;每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(1)英语老师随机抽了4个单词进行检测,求至少有3个是后两天学习过的单词的概率;
(2)某学生对后两天所学过的单词每个能默写对的概率为

正确答案
(1)设英语老师抽到的4个单词中,至少含有3个后两天学过的事件为A,则由题意可得
(2)由题意可得ξ可取0,1,2,3,则有P(ξ=0)
P(ξ=1)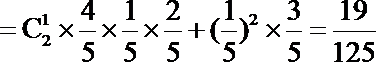
P(ξ=2) 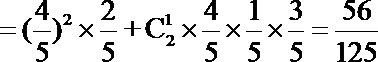
P(ξ=3)
所以ξ的分布列为:
故Eξ=0×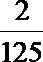
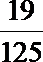
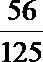
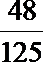
解析
解析已在路上飞奔,马上就到!
知识点
15.某地区为某类人员免费提供财会和计算机培训,参加培训者可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有





正确答案
2.7
解析
解析已在路上飞奔,马上就到!
知识点
19.某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
甲:19 20 21 23 25 29 32 33 37 41
乙:10 26 30 30 34 37 44 46 46 47
(1)用茎叶图表示上述两组数据,并分别求两块地抽取树苗的高度的平均数和中位数;
(2)绿化部门分配这


(3)现苗圃基地将甲、乙两块地的树苗合在一起,按高度分成一、二两个等级,每个等级按不同的价格出售.某市绿化部门下属的2个单位计划购买甲、乙两地种植的树苗.已知每个单位购买每个等级树苗所需费用均为5万元,且每个单位对每个等级树苗买和不买的可能性各占一半,求该市绿化部门此次采购所需资金总额
正确答案
(1)画出茎叶图如下:
①甲地树苗高度的平均数为

②甲地树苗高度的中位数为


(2)都来自乙苗圃的概率为
(3)






∴
∴
∴该市绿化部门此次采购的资金总额
解析
解析已在路上飞奔,马上就到!
知识点
8.将3名同学安排到



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错或不答都得0分,已知甲队3人每人答对的概率分别为


(1)求随机变量

(2)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率。
正确答案
(1)




解析
解析已在路上飞奔,马上就到!
知识点
20.设6张卡片上分别写有函数





(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片,则停止抽取,否则继续进行,求抽取次数
正确答案
解:(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,则
(2)



故ξ的分布列为



解析
解析已在路上飞奔,马上就到!
知识点
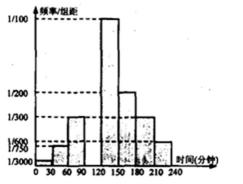
20.某校高一年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查。根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,l50),[150,180),[180,210),[210,240),得到频率分布直方图如下图。已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人。
(1)求n的值并求有效学习时间在[90,120)内的频率;
(2)如果把“学生晚上有效时间达到两小时”作为是
否充分利用时间的标准,对抽取的n名学生,请
补完整下列2×2列联表并判断是否有95%的把握
认为学生利用时间是否充分与走读、住宿有关?
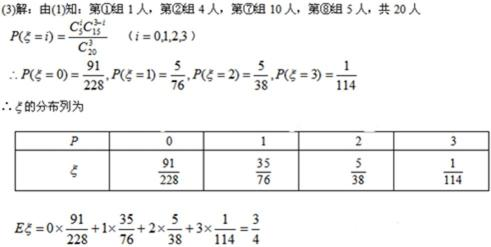
(3)若在第①组、第②组、第⑦组、第⑧组中共抽出3
人调查影响有效利用时间的原因,记抽到“有效学
习时间少于60分钟”的学生人数为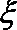
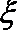
参考公式:K2=
参考列表:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设计某项工程,需要等可能地从4个向量a=(2,3)、b=(1,5)、c=(4,3)、d=(8,1)中任选两个来计算数量积,若所得数量积为随机变量ξ.
(1)求随机变量ξ≤19的概率;
(2)求随机变量ξ的分布列和期望E(ξ).
正确答案
(1)
a·b=2×1+3×5=17,
a·c=2×4+3×3=17,
a·d=2×8+3×1=19,
b·c=1×4+5×3=19
b·d=1×8+5×1=13,
c·d=4×8+3×1=35
P(ξ≤19)=P(ξ=19)+P(ξ=17)+P(ξ=13)=
∴数量积ξ≤19的概率为
(2)数量积ξ可能取值为13,17,19,35,
P(ξ=13)=

P(ξ=19)=
数量积ξ的分布列为
数量积ξ的期望E(ξ)=
解析
解析已在路上飞奔,马上就到!
知识点
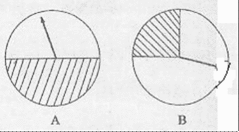
16.如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的

(1)记先转A转盘最终所得积分为随机量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。
正确答案
(1)X的取值分别是:0分,1000分,3000分
(2)由已知得,转动A盘得到积分的概率为
转动B盘得到积分的概率为
设先转A盘所得的积分为X分,先转B盘所得的积分为Y分,则有
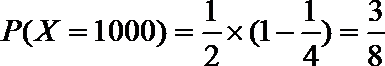
同理:
故先转A盘时,赢得积分平均水平较高。
解析
解析已在路上飞奔,马上就到!
知识点
18.现有A,B两球队进行友谊比赛,设A队在每局比赛中获胜的概率都是
(Ⅰ)若比赛6局,求A队至多获胜4局的概率;
(Ⅱ)若采用“五局三胜”制,求比赛局数ξ的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.前不久,省社科院发布了2013年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城市”.随后,树德中学校学生会组织部分同学,用“10分制”随机调查“新华西路”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.学校游园活动有这样一个游戏节目,甲箱子里装有3个白球、2个黑球;乙箱子里装有1个白球、2个黑球。这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在一次游戏中:①摸出3个白球的概率;②获奖的概率;
(Ⅱ)求在两次游戏中获奖次数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励
市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0. 4和0. 5 ;租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(I)求甲、乙两人所付租车费相同的概率;
(II)设甲、乙两人所付租车费之和为随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某单位从一所学校招收某类特殊人才.对
例如,表中运动协调能力良好且逻辑思维能力一般的学生有


(I) 求

(II)从参加测试的

(III)从参加测试的

生人数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析