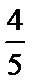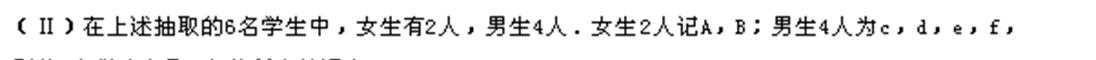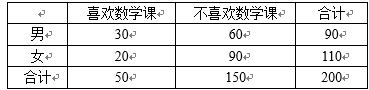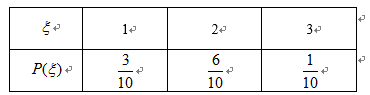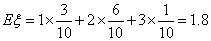- 概率与统计
- 共1631题
4.某旅游城市为向游客介绍本地的气温情况，绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月的平均最高气温约为15°C，B点表示四月的平均最低气温约为5°C。下面叙述不正确的是
正确答案
考查方向
解题思路
根据图中的最高气温和最低气温线观察分析。
易错点
审题要清晰，答案要求找不正确的；再者读图要细致，根据选择支语句加强讨论。
知识点
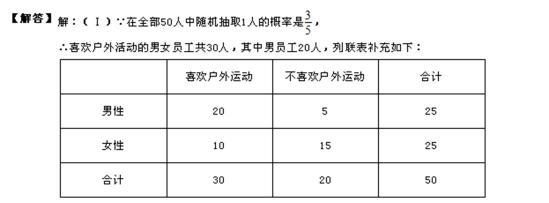
为了提高全民的身体素质，某地区增加了许多的户外运动设施为本地户外运动提供服务，为了进一步了解人们对户外运动的喜爱与否，随机对50人进行了问卷调查，已知在这50人中随机抽取1人抽到喜欢户外运动的概率为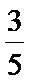
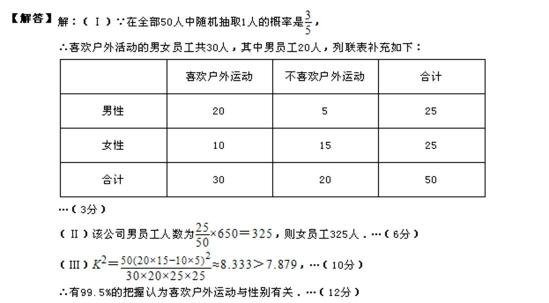
19.请将上面的列联表补充完整；
20.是否有99.5%的把握认为“喜欢户外运动与性别有关”？并说明你的理由；
21.根据分层抽样的方法从喜欢户外运动的人中抽取6人作为样本，从6人中随机抽取三人进行跟踪调查，那么这三人中至少有一名女性的概率是多少？
下面的临界值表仅供参考：
（参考公式：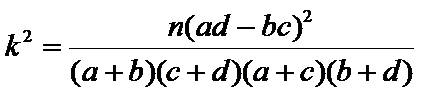
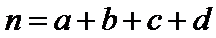
正确答案
见解析
解析
考查方向
解题思路
易错点
分层时候计算问题。再就是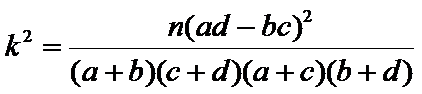
正确答案
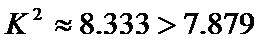
解析
考查方向
解题思路
易错点
分层时候计算问题。再就是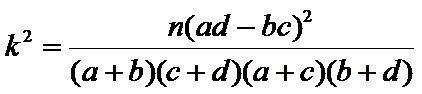
正确答案
解析
从六人中选出三人的方法数为n=20.其中三人中至少有一名女性的事件与没有女生的事件是对立事件，没有女生的基本事件数为4，所以概率为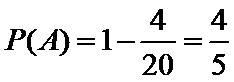
考查方向
解题思路
易错点
分层时候计算问题。再就是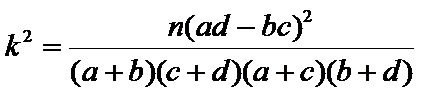
某工厂36名工人的年龄数据如下表。
工人编号 年龄
工人编号 年龄
工人编号 年龄
工人编号 年龄
1 40
2 44
3 40
4 41
5 33
6 40
7 45
8 42
9 43
10 36
11 31
12 38
13 39
14 43
15 45
16 39
17 38
18 36
19 27
20 43
21 41
22 37
23 34
24 42
25 37
26 44
27 42
28 34
29 39
30 43
31 38
32 42
33 53
34 37
35 49
36 39
18.用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；
19.计算（1）中样本的平均值
20.36名工人中年龄在
正确答案
（1）
解析
考查方向
解题思路
第一问，利用系统抽样抽取样本，知道第一组中抽取的编号，依次加上组距4，即可抽出所有样本数据。
易错点
系统抽样的选取办法，均值方差的计算。
正确答案
解析
方差为
考查方向
解题思路
第二问，直接利用均值和方差的公式计算即可。
易错点
系统抽样的选取办法，均值方差的计算。
正确答案
（3）
解析
考查方向
解题思路
第三问，利用第二问，得出均值和标准差之后，找到所在区域中的数据个数，然后估算出所占比例即可。
易错点
系统抽样的选取办法，均值方差的计算。
某班同学
年龄段分组
[20，25）
[25，30）
[30，35）
[35，
[40，45）
频数
300
320
160
160
40
20
19.在答题卡上作出这些数据的频率分布直方图；
20.估计年龄段的“低头族”的平均年龄（同一组中的数据用该组区间的中点值作代表）；
21.从年龄段在[25，35）的“低头族”中采用分层抽样法抽取6人接受采访，并从6人中随机选取2人作为嘉宾代表，求选取的2名嘉宾代表中恰有1人年龄在[25，30）岁的概率．
正确答案
略
正确答案
设“低头族”平均年龄为
则
正确答案
略
8．某学校共有老、中、青职工200人，其中有老年职工60人，中年职工人数与青年职工人数相等．现采用分层抽样的方法抽取部分职工进行调查，已知抽取的老年职工有12人，则抽取的青年职工应有（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况，随机抽查了该市当天
若网购金额超过
义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为
（1）试确定
（2）该营销部门为了进一步了解这
达人”中用分层抽样的方法确定
正确答案
见解析。
解析
(1)根据题意，有
解得
补全频率分布直方图如图所示。
（2）用分层抽样的方法，从中选取
其中“网购达人”有
故
所
知识点
给出下列四个命题，其中假命题是（ ）
A从匀速传递的新产品生产流水线上，质检员每10分钟从中抽取一件新产品进行某项指标检测，这样的抽样是分层抽样；
B样本方差反映了样本数据与样本平均值的偏离程度；
C在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；
D设随机变量
正确答案
解析
.选项A中的抽样为系统抽样，故此命题为假命题.其它选项为真命题.故选A
知识点
给出以下四个命题：
①已知命题
②圆
③在某项测量中，测量结果
④某企业有职工150人，其中高级职称15人，中级职称45人，一般职员90人，若用分层抽样的方法抽出一个容量为30的样本，则一般职员抽出20人.
其中正确命题的序号为_________（把你认为正确的命题序号都填上）
正确答案
解析
略
知识点
16.（本小题满分13分）某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团)：
学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从三个社团成员中抽取18人，结果拳击社被抽出了6人.
（1）求拳击社团被抽出的6人中有5人是男生的概率；
（2）设拳击社团有X名女生被抽出，求X的分布列.
正确答案
见解析。
解析
（1）由于按分层抽样的方法从三个社团成员中抽取18人，拳击社被抽出了6人，
∴
∴m＝2.
设A为“拳击社团被抽出的6人中有5人是男生”，
则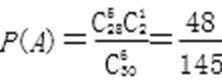
（2）由题意可知：X＝0,1,2，
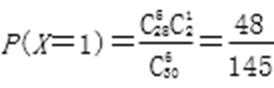
X的分布列为
知识点
为考察高中生的性别与是否喜欢数学课程之间的关系，在我市某普通中学高中生中随机抽取200名学生，得到如下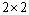
（1）根据独立性检验的基本思想，约有多大的把握认为“性别与喜欢数学课之间有关系”？
（2）若采用分层抽样的方法从不喜欢数学课的学生中随机抽取5人，则男生和女生抽取的人数分别是多少？
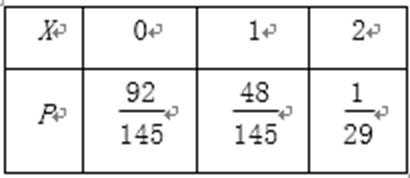
（3）从（2）随机抽取的5人中再随机抽取3人，该3人中女生的人数记为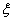
正确答案
见解析。
解析
（1）∵
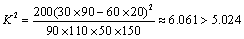
∴约有97.5%以上的把握认为“性别与喜欢数学课之间有关系”.
（2）男生抽取的人数有：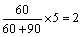
女生抽取的人数各有：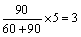
（3）由（2）可知，男生抽取的人数为2人，女生抽取的人数为3人，
所以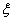
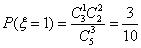
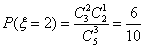
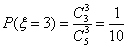
所以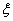
所以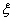
知识点
某学校高一、高二、高三共有2400名学生，为了调查学生的课余学习情况，拟采用分层抽样的方法抽取一个容量为120的样本.已知高一有820名学生，高二有780名学生，则在该学校的高三应抽取____________名学生。
正确答案
40
解析
略
知识点
以下五个命题
①从匀速传递的产品生产流水线上，质检员每10分钟0020从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样
②样本方差反映了样本数据与样本平均值的偏离程度
③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好
④在回归直线方程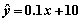
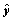
⑤在一个2×2列联表中，由计算得k2=13.079,则其两个变量间有关系的可能性是90%以上.
其中正确的是
正确答案
解析
略
知识点
某班有甲、乙两个学习小组，两组的人数如下：
现采用分层抽样的方法（层内采用简单随机抽样）从甲、乙两组中共抽取
（1）求从甲组抽取的同学中恰有
（2）记
正确答案
见解析
解析
（1）解：依题意，甲、乙两组的学生人数之比为 
所以，从甲组抽取的学生人数为
设“从甲组抽取的同学中恰有
则 
故从甲组抽取的同学中恰有
（2）解：随机变量
所以，随机变量
………………11分
知识点
某校高二年级进行社会实践，对[25, 55]岁的人群随机抽取n个人进行了一次是否开通“微信”， 若开通“微信”的为“时尚族”，否则称为“非时尚族”，通过调查分别得到如图1所示统计表，如图2所示各年龄段人数频率分布直方图：
请完成以下问题：
（1）补全频率直方图，并求n，a，p的值；
（2）从[40，45）岁和[45，50）岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络“时尚达人”大赛，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁得人数为ξ，求ξ的分布列和数学期望E（X）.
正确答案
见解析
解析
（1）第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,所以高为
第一组的人数为
频率为0.04×5=0.2，所以
第四组的频率为0.03×5=0.15，人数为1000×0.15=150，
（2）因为[40,45)岁与[45,50)岁年龄段的“时尚族”的比值为60:30=2:1，所以分层抽样法抽取18人，[40,45)岁中有12人，[45,50)岁中有6人，随机变量
数学期望为
知识点
扫码查看完整答案与解析