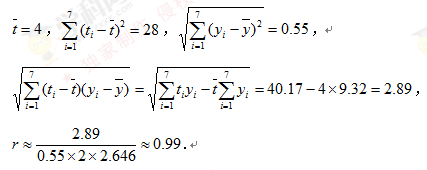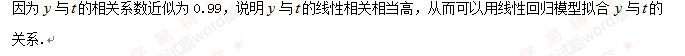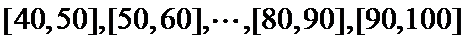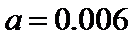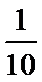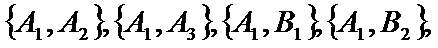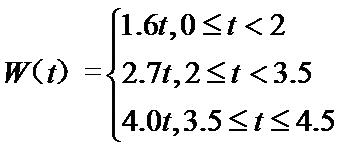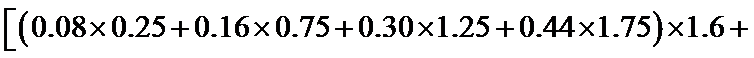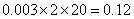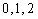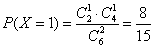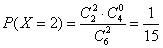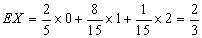- 概率与统计
- 共1631题
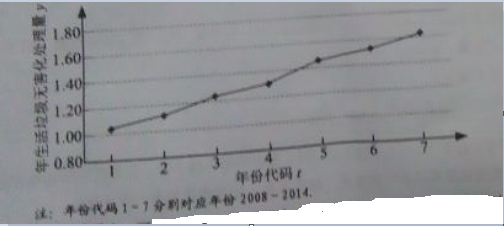
18.下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
(I)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明
(II)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量。
正确答案
解:(Ⅰ)由折线图这数据和附注中参考数据得
所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
知识点
19.某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记

(I)求
(II)若要求

(III)以购买易损零件所需费用的期望值为决策依据,在

正确答案
19.(I)x的取值为16,17,18,19,20,21,22
P(x=16)=(
P(x=17)=
P(x=18)= (

P(x=19)= 2×


P(x=20)=(

P(x=21)= 2×
P(x=22)= 
x的分布列:
(II)
p(x≤18)=
p(x≤19)=
(III)由(I)分布列:p(x≤19)=
买19个所需费用期望EX1=200×19×
+(200×19+500×2) ×
买20个所需费用期望EX2=200×20×
+(200×20+2×500) ×
∴EX1<EX2 ∴ 买19个更合适.
知识点
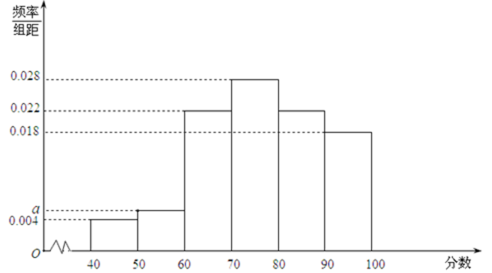
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
18.求频率分布图中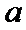
19.估计该企业的职工对该部门评分不低于80的概率;
20.从评分在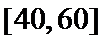
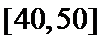
正确答案
(Ⅰ)0.006
解析
(Ⅰ)因为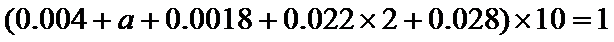
考查方向
解题思路
根据所给统计量计算求得
易错点
计算错误,对相关概念理解错误
正确答案
(Ⅱ)
解析
(Ⅱ)由所给频率分布直方图知,50名受访职工评分不低于80的频率为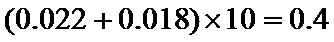
所以该企业职工对该部门评分不低于80的概率的估计值为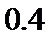
解题思路
根据频率分布直方图求得
易错点
频率求错,读图能力提信息时马虎大意。
正确答案
(Ⅲ)
解析
(Ⅲ)受访职工评分在[50,60)的有:50×0.006×10=3(人),即为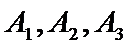
受访职工评分在[40,50)的有: 50×0.004×40=2(人),即为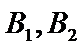
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是
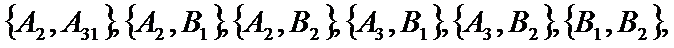
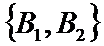
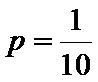
考查方向
解题思路
根据题意,按区间分别求概率
易错点
分类时错误,区间求概率时错误
A、B、C三个班共有100名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:小时);
17.试估计C班的学生人数;
18.从A班和C班抽出的学生中,各随机选取一人,A班选出的人记为甲,C班选出的人记为乙,假设所有学生的锻炼时间相对独立,求该周甲的锻炼时间比乙的锻炼时间长的概率;
19.再从A、B、C三个班中各随机抽取一名学生,他们该周的锻炼时间分别是7,9,8.25(单位:小时),这3个新数据与表格中的数据构成的新样本的平均数记



正确答案
(1)40;
解析
(1)由已知可得,抽出的20名学生中,来自C班的学生有8名,根据分层抽样方法,C班的学生
考查方向
解题思路
(Ⅰ)根据图表判断C班人数,由分层抽样的抽样比计算C班的学生人数;
(Ⅱ)根据题意列出“该周甲的锻炼时间比乙的锻炼时间长”的所有事件,由独立事件概率公式求概率.
(Ⅲ)根据平均数公式进行判断即可.
易错点
运用逆向思维的方法(正难则反)求解,应用此公式时,一定要分清事件的对立事件到底是什么事件,不能重复或遗漏.
正确答案
(2)
解析
考查方向
解题思路
(Ⅰ)根据图表判断C班人数,由分层抽样的抽样比计算C班的学生人数;
(Ⅱ)根据题意列出“该周甲的锻炼时间比乙的锻炼时间长”的所有事件,由独立事件概率公式求概率.
(Ⅲ)根据平均数公式进行判断即可.
易错点
运用逆向思维的方法(正难则反)求解,应用此公式时,一定要分清事件的对立事件到底是什么事件,不能重复或遗漏.
正确答案
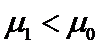
解析
考查方向
解题思路
(Ⅰ)根据图表判断C班人数,由分层抽样的抽样比计算C班的学生人数;
(Ⅱ)根据题意列出“该周甲的锻炼时间比乙的锻炼时间长”的所有事件,由独立事件概率公式求概率.
(Ⅲ)根据平均数公式进行判断即可.
易错点
运用逆向思维的方法(正难则反)求解,应用此公式时,一定要分清事件的对立事件到底是什么事件,不能重复或遗漏.
4.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程

正确答案
解析
由已知得




考查方向
解题思路
由题意可知X平均和y平均,可得回归方长,把X=15代入方程求得y值即可。
易错点
线性回归方程列错,计算能力弱
知识点
5.身穿红、黄两种颜色衣服的各有两人,现将这4人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )种。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知样本:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 以下茎叶图记录了甲,乙两组各五名学生在一次英语听力测

已知甲组数据的中位数为


正确答案
解析
将两组数据列出甲组数据:9,12,10+x,24,27;乙组数据:9,15,10+y,18,24.由上面数据及题意可知甲中的中位数为



A选项不正确,B选项不正确,D选项不正确,所有选C选项.
考查方向
解题思路
1、先将两组数据列出来,然后按题目要求找出中位数2、平均数直接代入计算即可. A选项不正确,B选项不正确,D选项不正确,所有选C选项.
易错点
1、本题中拟出各组数据易将十位数字弄错 . 2、本题易将中位数和众数混淆,导致题目解答出错.
知识点
19.心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学 (男30女20), 给所有同学几何题和代数题各一题,让各位同
(I)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(II)经过多次测试后,女生甲每次解答一道几何题所用的时间在5—7分钟,女生乙每次解答一道几何题所用的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(III)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、 乙两女生被抽到的人数为


附表及
正确答案
(Ⅰ)


解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)构造几何概型模型(3)确定随机变量,求随机变量的期望. (Ⅰ)由表中数据得


(Ⅱ)设甲、乙解答一


设事件


(Ⅲ)由题可知在选择做几何题的8名女生中任意抽取两人,抽取方法有








考查方向
解题思路
本题考查导数的性质,解题步骤如下: 1、求
易错点
1、第一问相关性分析数据容易计算错误. 2、第二问中的概率计算中的基本事件查找不清,易造成计算错误. 3、第三问中的分布列的随机变量的值对应的概率在计算时易出现出现错误.
知识点
某城市居民月生活用水收费标准为
(t为用水量,单位:吨;W为水费,单位:元),
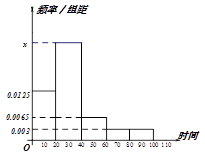
从该市抽取的100户居民的月均用水量的频率分布直方图如图所示.
21.求这100户居民的月均用水量的中位数及平均水费;
22.连续10个月,每月从这100户中随机抽取一户,若抽到的用户当月所交水费少于9.45元,则对其予以奖励,设X为获奖户数,求X的数学期望.
正确答案
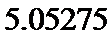
解析
试题分析:本题属常见的概率问题,在审题时一要会识图,二要从题意中提炼出概率事件是独立重复实验再下手去做。其难度和其它概率问题一样难度适中,主要是题意的理解。
由频率分布直方图可知,月平均用水量的中位数为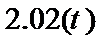
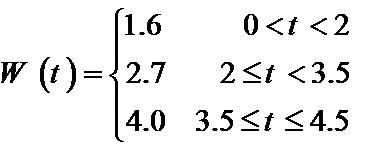
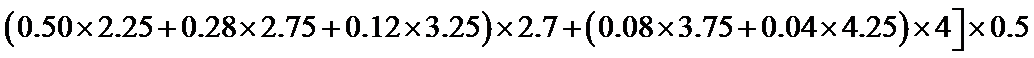
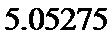
考查方向
本题主要考查统计与概率的相关知识,其中包括频率分布直方图,独立重复概率计算,分布列以及期望的计算等知识,意在考查考生的识图能力,数据处理能力,思维能力,计算能力。
解题思路
本题考查概率和期望的计算,解题步骤如下:
1、从频率分布直方图读出不同水量用户的频数,再结合分段函数完成第一问即可。
2、找X,计算概率,列分布列,再计算期望。
易错点
1、第一问结合分段函数和频率分布直方图得出数据时易出错。
2、第二问不易把此概率问题看成二项分布模型,再就是期望的计算也是学生易错点之一。
正确答案
9.4
解析
试题分析:本题属常见的概率问题,在审题时一要会识图,二要从题意中提炼出概率事件是独立重复实验再下手去做。其难度和其它概率问题一样难度适中,主要是题意的理解。
依题意知这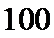
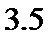
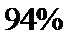
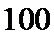
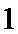
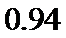
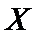
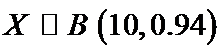
所以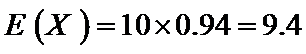
考查方向
本题主要考查统计与概率的相关知识,其中包括频率分布直方图,独立重复概率计算,分布列以及期望的计算等知识,意在考查考生的识图能力,数据处理能力,思维能力,计算能力。
解题思路
本题考查概率和期望的计算,解题步骤如下:
1、从频率分布直方图读出不同水量用户的频数,再结合分段函数完成第一问即可。
2、找X,计算概率,列分布列,再计算期望。
易错点
1、第一问结合分段函数和频率分布直方图得出数据时易出错。
2、第二问不易把此概率问题看成二项分布模型,再就是期望的计算也是学生易错点之一。
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是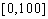
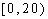
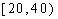
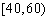
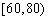
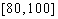
(1)求直方图中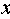
(2)如果上学路上所需时间不少于60分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
(3)现有6名上学路上时间小于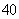
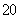
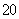
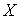
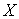
正确答案
见解析。
解析
(1)由直方图可得:
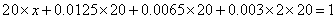
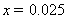
(2)新生上学所需时间不少于60分钟的频率为:
因为
所以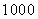
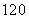
(3)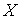
所以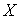
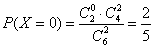
所以
知识点
在某批次的某种灯泡中,随机地抽取200个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
(1)根据频率分布表中的数据,写出a,b的值;
(2)某人从灯泡样品中随机地购买了
(3)某人从这个批次的灯泡中随机地购买了3个进行使用,若以上述频率作为概率,用X表示此人所购买的灯泡中次品的个数,求X的分布列和数学期望.
正确答案
见解析
解析
(1)解:

(2)解:由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,所以优等品、正品和次品的比例为



(3)解:


从本批次灯泡中购买3个,可看成3次独立重复试验,
所以



所以随机变量


(注:写出


知识点
10.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析