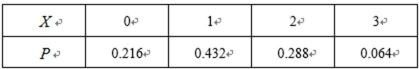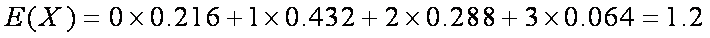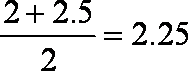- 概率与统计
- 共1631题
第30届夏季奥运会将于2012年7月27日在伦敦举行, 当地某学校招募了8名男志愿者和12名女志愿者. 将这20名志愿者的身高编成如下茎叶图(单位:cm):
若身高在180cm以上(包括180cm)定义为“高个子”, 身高在180cm以下(不包括180cm)定义为“非高个子”, 且只有“女高个子”才能担任“礼仪小组”.
(1) 如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人, 再从这5人中选2人, 那么至少有一人是“高个子”的概率是多少?
(2) 若从所有“高个子”中选3名志愿者, 用X表示所选志愿者中能担任“礼仪小组”的人数, 试写出X的分布列, 并求X的数学期望.
正确答案
(1)
解析
解析:
知识点
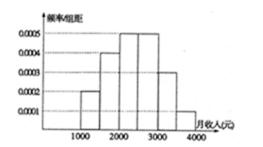
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500) 单位:元)
(1)估计居民月收入在[1500,2000)的概率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在[2500,3500)的居民数X的分布和数学期望。
正确答案
见解析。
解析
(1)依题意及频率分布直方图知,居民月收入在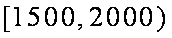
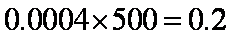
(2)频率分布直方图知,中位数在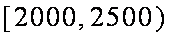
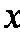
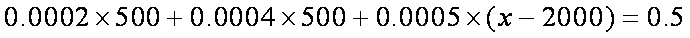
解得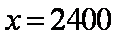
(3)居民月收入在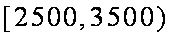
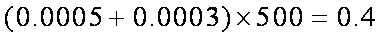
由题意知,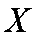
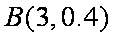
因此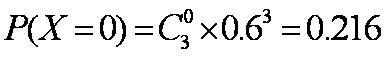
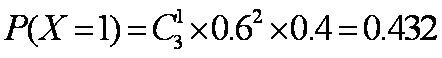
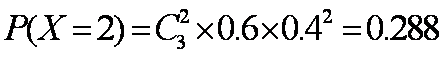
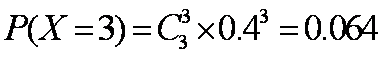
故随机变量X的分布列为
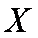
知识点
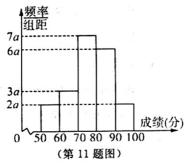
100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则测试成绩落在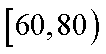
正确答案
50
解析
略
知识点
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,

正确答案
解析
由题意可知





知识点
某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次当前投资生活方式——“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
(1)求n,a,p的值;
(2)从


正确答案
(1)n=200,a=60,p=0.065 (2)2
解析
(1)年龄在[25,30)的总人数为
根据频率分布直方图,总人数为
年龄在[40,45)的人数为
所以 
因为年龄在[30,35)的人数的频率为

所以
(2)依题抽取年龄在[40,45) 之间6人,
抽取年龄在[45,50)之间3人,…………………………………7分





所以 
知识点
对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图,则估计此样本的众数、中位数分别为()
正确答案
解析
样本的众数为最高矩形底边中点对应的横坐标,为
中位数是频率为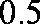
由于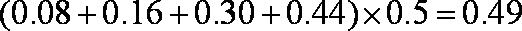
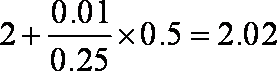
知识点
某校从参加高一年级期末考试的学生中抽出



(1)求第四小组的频率;
(2)从成绩是


正确答案
(1)0.3;(2)
解析
(1)因为各组的频率和等于1,故第四组的频率:

(2)设人数为
Ex=
知识点
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85), 第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示。
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(ⅱ) 学校决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有

正确答案
见解析
解析
解:(1)第三组的频率为0.06
第四组的频率为0.04
第五组的频率为0.02
(2)(ⅰ)设M:学生甲和学生乙同时进入第二轮面试
P(M)=

(ⅱ)

知识点
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数位12,则抽取的学生人数是__________。
正确答案
解析
后两个小组的频率为




知识点
对某校高三年级学生参加社区服务次数进行统计,随机抽取

(1)求出表中
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
见解析
解析
解析:(1)由分组



所以
因为频数之和为



因为


(2)因为该校高三学生有240人,分组

所以估计该校高三学生参加社区服务的次数在此区间内的人数为
(3)这个样本参加社区服务的次数不少于20次的学生共有
设在区间



则任选


而两人都在

所以所求概率为

知识点
19.某市公租房的房源位于
(Ⅰ)恰有2人申请
(Ⅱ)申请的房源所在片区的个数
正确答案
(Ⅰ)所有可能的申请方式有


从而恰有2人申请

(Ⅱ)




综上知, 
从而有
解析
解析已在路上飞奔,马上就到!
知识点
6.某路段的雷达测速区检测点,对过往汽车的车速进行检测所得结果进行抽样分析,并绘制如图所示的时速(单位km/h)频率分布直方图,若在某一时间内有200辆汽车通过该检测点,请你根据直方图的数据估计在这200辆汽车中时速超过65km/h的约有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图所示程序框图,其作用是输入空间直角坐标平面中一点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 如图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若80分以上为优秀,根据图形信息可知:这次考试的优秀率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为________.
正确答案
100
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析