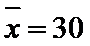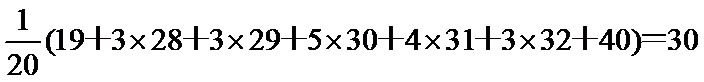- 概率与统计
- 共1631题
4. 某次体检,

(米)
正确答案
知识点
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费



22.根据散点图判断,

23.根据(I)的判断结果及表中数据,建立y关于x的回归方程;
24.已知这种产品的年利润z与x,y的关系为
(i)当年宣传费
(ii)当年宣传费
附:对于一组数据




正确答案
(Ⅰ)


解析
(Ⅰ)由散点图可以判断,


考查方向
解题思路
试题分析:(Ⅰ)由散点图及所给函数图像即可选出适合作为拟合的函数;
易错点
本题在寻求拟合函数比较易错
正确答案
(Ⅱ)
解析
(Ⅱ)令




∴
∴


∴


考查方向
易错点
在非线性回归方程进行预报预测;应用易错.
正确答案
(Ⅲ)46.24
解析
(Ⅲ)(ⅰ)由(Ⅱ)知,当



(ⅱ)根据(Ⅱ)的结果知,年利润z的预报值

∴当



故宣传费用为46.24千元时,年利润的预报值最大.……12分
考查方向
解题思路
(Ⅲ)(ⅰ)利用



易错点
在非线性回归方程进行预报预测;应用易错.
某工厂36名工人的年龄数据如下表。
工人编号 年龄
工人编号 年龄
工人编号 年龄
工人编号 年龄
1 40
2 44
3 40
4 41
5 33
6 40
7 45
8 42
9 43
10 36
11 31
12 38
13 39
14 43
15 45
16 39
17 38
18 36
19 27
20 43
21 41
22 37
23 34
24 42
25 37
26 44
27 42
28 34
29 39
30 43
31 38
32 42
33 53
34 37
35 49
36 39
18.用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
19.计算(1)中样本的平均值

20.36名工人中年龄在

正确答案
(1)








解析

考查方向
解题思路
第一问,利用系统抽样抽取样本,知道第一组中抽取的编号,依次加上组距4,即可抽出所有样本数据。
易错点
系统抽样的选取办法,均值方差的计算。
正确答案


解析



方差为


考查方向
解题思路
第二问,直接利用均值和方差的公式计算即可。
易错点
系统抽样的选取办法,均值方差的计算。
正确答案
(3)

解析








考查方向
解题思路
第三问,利用第二问,得出均值和标准差之后,找到所在区域中的数据个数,然后估算出所占比例即可。
易错点
系统抽样的选取办法,均值方差的计算。
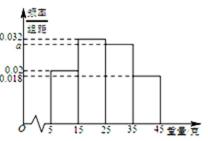
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取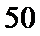
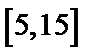
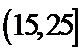
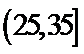
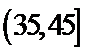
19.求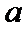
20.从盒子中随机抽取
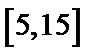

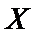
正确答案
估计盒子中小球重量的平均值约为
解析
(Ⅰ)由题意,得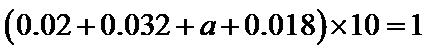
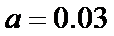
又由最高矩形中点的的横坐标为20,可估计盒子中小球重量的众数约为20(克),
而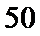
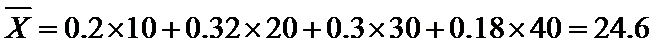
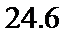
考查方向
解题思路
根据频率分布直方图求出a的值,然后根据直方图估计盒子中小球重量的众数与平均值;
易错点
不会根据频率分布直方图估计平均数;
正确答案
(2)

(或者
解析
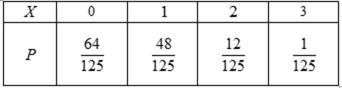
(Ⅱ)利用样本估计总体,该盒子中小球重量在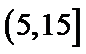
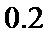
则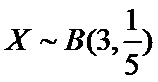

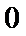
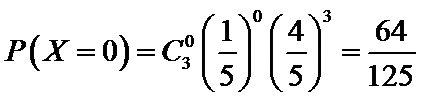
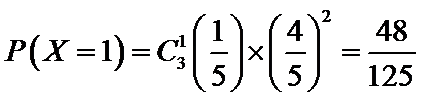
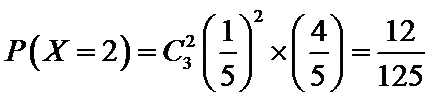
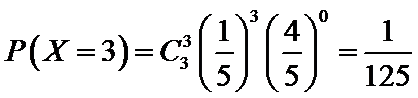

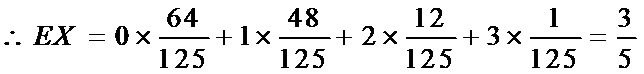
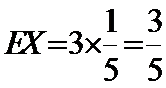
考查方向
解题思路
根据题意判断出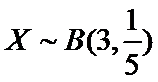
易错点
看不出二项分布导致运算很麻烦。
3.重庆市2013年各月的平均气温(
则这组数据的中位数是( )
正确答案
解析
从茎叶图知所有数据为8,9,12,15,18,20,20,23,23,28,31,32,
中间两个数为20,20,故中位数为20,选B..
考查方向
解题思路
本题通过考查茎叶图的知识,考查样本数据的数字特征,考查学生的数据处理能力.
易错点
数据大小的排列
知识点
党的领导与政府的领导( )。
A.在性质、职能方面没有区别,在加强公安工作的目标上是一致的,大政方针是统一的
B.在各自对公安机关的领导中,要互相保证,而不能互相冲击
C.党委对公安机关的领导是从政治方向、思想路线和重大决策上保证各级政府对公安机关领导的正确性
D.各级政府对同级公安机关的领导,是通过行政管理工作保证党的路线、方针、政策、重大决策的切实贯彻实施
正确答案
B,C,D
解析
[解析] 党的领导与政府领导虽然在性质、职能等方面有区别,但加强公安工作的目标是一致的,大政方针是统一的。因此,在各自对公安机关的领导中,要互相保证,而不能互相冲击。党委对公安机关的领导是从政治方向、思想路线和重大决策上保证各级政府对公安机关领导的正确性;各级政府对同级公安机关的领导,是通过行政管理工作保证党的路线、方针、政策、重大决策的切实贯彻实施。故选BCD。
某车间20名工人年龄数据如下表:
21.求这20名工人年龄的众数与平均数;
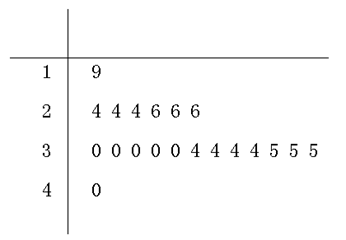
22.以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
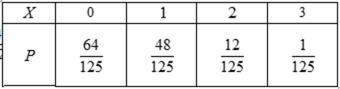
23.从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率。
正确答案
众数是30;
解析
(Ⅰ) 由题意可知,这20名工人年龄的众数是30,
这20名工人年龄的平均数为
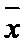
考查方向
解题思路
根据众数和平均数的定义,即可得出;
易错点
熟记众数和平均数的概念.
正确答案
见解析
解析
这20名工人年龄的茎叶图如图所示:
考查方向
解题思路
根据画茎叶图的步骤,画图即可;
易错点
无
正确答案
解析
记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3则从这6人中随机抽取2人的所有可能为
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A1,B3},{A2,B1},{A2,B2},{A2,B,3},{A3,B1},
{A3,B2},{A,3,B3},{B1,B2},{B1,B3},{B2,B3}共15种。
满足题意的有{A1,A2},{A1,A3},{A2,A3}3种,
故所求的概率为P=
考查方向
解题思路
利用枚举法,将6人中随机抽取2人的所有可能的情况列举出来,再求概率.
易错点
古典概型中使用枚举时,要注意不重不漏.
某车间20名工人年龄数据如下表:
21.求这20名工人年龄的众数与平均数;
22.以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
23.从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率。
正确答案
众数是30;
解析
(Ⅰ) 由题意可知,这20名工人年龄的众数是30,
这20名工人年龄的平均数为

考查方向
解题思路
根据众数和平均数的定义,即可得出;
易错点
熟记众数和平均数的概念.
正确答案
见解析
解析
这20名工人年龄的茎叶图如图所示:
考查方向
解题思路
根据画茎叶图的步骤,画图即可;
易错点
无
正确答案
解析
记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3则从这6人中随机抽取2人的所有可能为
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A1,B3},{A2,B1},{A2,B2},{A2,B,3},{A3,B1},
{A3,B2},{A,3,B3},{B1,B2},{B1,B3},{B2,B3}共15种。
满足题意的有{A1,A2},{A1,A3},{A2,A3}3种,
故所求的概率为P=
考查方向
解题思路
利用枚举法,将6人中随机抽取2人的所有可能的情况列举出来,再求概率.
易错点
古典概型中使用枚举时,要注意不重不漏.
9.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分. 两人4局的得分情况如下:
(Ⅰ)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求
(Ⅱ)如果




(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
正确答案
(Ⅰ)15
(Ⅱ)

(Ⅲ) 


解析
(Ⅰ)解:由题意,得

因为在乙的4局比赛中,随机选取1局,则此局得分小于6分的概率不为零,
所以
又因为

所以
所以
(Ⅱ)解:设 “从甲、乙的4局比赛中随机各选取1局,且得分满足
记甲的4局比赛为



为



则从甲、乙的4局比赛中随机各选取1局,所有可能的结果有16种, 它们是:















而事件








因此事件

(Ⅲ)解:



考查方向
解题思路
1、第一问由选取1局得分小于6分的概率不为零,可知x,y取值均为小于或等于5的自然数;结合乙的平均得分高于甲的平均得分确定的
2、第二问通过列举从甲、乙的4局比赛中随机各选取1局,所有可能的结果可以找出满足题意的事件数目,最终求出其概率。
3、第三问通过平均分相同得出

易错点
不能从题目中提取出

知识点
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费

表中w1 =


21.根据散点图判断,y=a+bx与y=c+d
22.根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
23.以知这种产品的年利率z与x、y的关系为z=0.2y-x。根据(Ⅱ)的结果回答下列问题:
(i) 年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii) 年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据(u1 v1),(u2 v2)…….. (un vn),其回归线v=
正确答案
正确答案
正确答案
正确答案
知识点
22.写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
正确答案
用二分法求方程的近似值一般取区间[a,b]具有以下特征:
f(a)<0,f(b)>0.
由于f(1)=13-1-1=-1<0,
f(1.5)=1.53-1.5-1=0.875>0,
所以取[1,1.5]中点
相应的程序框图是:
程序:a=1
b=1.5
c=0.001
DO
x=(a+b)2
f(a)=a∧3-a-1
f(x)=x∧3-x-1
IF f(x)=0 THEN
PRINT “x=”;x
ELSE
IF f(a)*f(x)<0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS(a-b)<=c
PRINT “方程的一个近似解x=”;x
END
解析
解析已在路上飞奔,马上就到!
知识点
某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
(1) 求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘估计公式分别为:
正确答案
(1) 回归方程为=0.5t+2.3.
(2)预测该地区2015年农村居民家庭人均纯收入为6.8千元。
解析
知识点
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据

正确答案
解析
由回归方程为


知识点
扫码查看完整答案与解析