- 概率与统计
- 共1631题
某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的宣传费
22.根据散点图判断，
23.根据（I）的判断结果及表中数据，建立y关于x的回归方程；
24.已知这种产品的年利润z与x，y的关系为
（i）当年宣传费
（ii）当年宣传费
附：对于一组数据
正确答案
（Ⅰ）
解析
（Ⅰ）由散点图可以判断，
考查方向
解题思路
试题分析：（Ⅰ）由散点图及所给函数图像即可选出适合作为拟合的函数；
易错点
本题在寻求拟合函数比较易错
正确答案
（Ⅱ）
解析
（Ⅱ）令
∴
∴
∴
考查方向
易错点
在非线性回归方程进行预报预测；应用易错.
正确答案
（Ⅲ）46.24
解析
（Ⅲ）（ⅰ）由（Ⅱ）知，当
（ⅱ）根据（Ⅱ）的结果知，年利润z的预报值
∴当
故宣传费用为46.24千元时，年利润的预报值最大.……12分
考查方向
解题思路
（Ⅲ）（ⅰ）利用
易错点
在非线性回归方程进行预报预测；应用易错.
某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费
表中w1 =
21.根据散点图判断，y=a+bx与y=c+d
22.根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
23.以知这种产品的年利率z与x、y的关系为z=0.2y-x。根据（Ⅱ）的结果回答下列问题：
（i） 年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii） 年宣传费x为何值时，年利率的预报值最大？
附：对于一组数据（u1 v1）,（u2 v2）…….. （un vn）,其回归线v=
正确答案
正确答案
正确答案
国内某知名大学有男生14000人，女生10000人.该校体育学院想了解本校学生的运动状况，根据性别采取分层抽样的方法从全校学生中抽取120人
男生平均每天运动的时间分布情况：
女生平均每天运动的时间分布情况：
19.请根据样本估算该校男生平均每天运动的时间（结果精确到
20.若规定平均每
为“非运动达人”.
①请根据样本估算该校“运动达人”的数量；
②请根据上述表格中的统计数据填写下面
误的概率不超过
参考公式：
参考数据：
正确答案
(1) 
解析
（Ⅰ）由分层抽样得：男生抽取的人数为
则该校男生平均每天运动的时间为：
故该校男生平均每天运动的时间约为
考查方向
解题思路
根据题中给出的数据估计该校男生平均每天运动的时间约为
易错点
不会根据频率分布直方图估计平均数；
正确答案
(2) ①4000;
②
解析
（Ⅱ）①样本中“运动达人”所占比例是
②由表格可知：
故
故在犯错误的概率不超过
考查方向
解题思路
先列出列联表后计算
易错点
处理数据列
正确答案
知识点
1．以下四个命题：
①从匀速传递的产品生产流水线上，质检员每20分钟从中抽取一件产品进行某项指标检测 ，这样的抽样是分层抽样。
②两个随机变量相关性越强，则相关系数的绝对值越接近于1
③在回归直线方程
④对分类变量X与Y，它们的随机变量K2的观测值k来说，k越小，“X与Y有关系”的把握程度越大
以上命题中，正确的是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22．写出用二分法求方程x3－x－1=0在区间［1，1．5］上的一个解的算法（误差不超过0．001），并画出相应的程序框图及程序．
正确答案
用二分法求方程的近似值一般取区间［a，b］具有以下特征：
f（a）＜0，f（b）＞0．
由于f（1）=13－1－1=－1＜0，
f（1．5）=1．53－1．5－1=0．875＞0，
所以取［1，1．5］中点
相应的程序框图是：
程序：a=1
b=1．5
c=0．001
DO
x=（a+b）2
f（a）=a∧3－a－1
f（x）=x∧3－x－1
IF f（x）=0 THEN
PRINT “x=”；x
ELSE
IF f（a）*f（x）＜0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS（a－b）＜=c
PRINT “方程的一个近似解x=”；x
END
解析
解析已在路上飞奔，马上就到！
知识点
9．在一组样本数据（x1，y1），（x2，y2），…，（xn，yn）（n≥2，x1,x2,…,xn不全相等）的散点图中，若所有样本点（xi，yi）（i=1,2,…,n）都在直线y=
A－1
B0
C
D1
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
某地区2007年至2013年农村居民家庭人均纯收入y(单位：千元)的数据如下表：
(1) 求y关于t的线性回归方程；
(2)利用(1)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入。
附：回归直线的斜率和截距的最小二乘估计公式分别为：
正确答案
(1) 回归方程为＝0.5t＋2.3.
(2)预测该地区2015年农村居民家庭人均纯收入为6.8千元。
解析
知识点
设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据
Ay与x具有正的线性相关关系
B回归直线过样本点的中心
C若该大学某女生身高增加1cm，则其体重约增加
D若该大学某女生身高为170cm，则可断定其体重比为
正确答案
解析
由回归方程为
知识点
已知
正确答案
70
解析
略
知识点
某学生课外活动兴趣小组对两个相关变量收集到5组数据如下表：
由最小二乘法求得回归方程为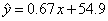
正确答案
68
解析
略
知识点
某工厂的某种型号机器的使用年限x和所支出的维修费用y（万元）有下表的统计资料：
根据上表可得回归方程
正确答案
解析
略
知识点
以下五个命题
①从匀速传递的产品生产流水线上，质检员每10分钟0020从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样
②样本方差反映了样本数据与样本平均值的偏离程度
③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好
④在回归直线方程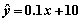
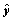
⑤在一个2×2列联表中，由计算得k2=13.079,则其两个变量间有关系的可能性是90%以上.
其中正确的是
正确答案
解析
略
知识点
某研究机构对高三学生的记忆力x和判断力y进行统计分析，得下表数据：
根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
其中
A7
B
C8
D
正确答案
解析
略
知识点
已知x与y之间的几组数据如下表：
假设根据上表数据所得线性回归直线方程为
A
B
C
D
正确答案
解析
略
知识点
扫码查看完整答案与解析