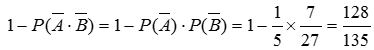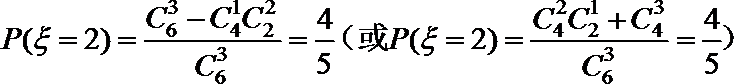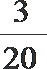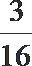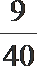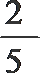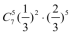- 概率与统计
- 共1631题
9.有2本不同的数学书和3本不同的英语书分给五位同学,每人一本,则甲、乙两位同学恰有一位分到数学书的概率( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从
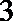
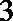
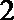
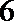


(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.
正确答案
解:(Ⅰ)设甲、乙闯关成功分别为事件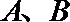
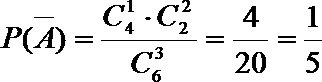
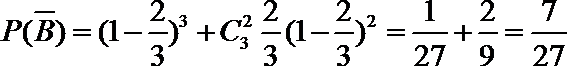
所以,甲、乙至少有一人闯关成功的概率是:
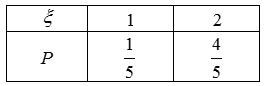
(Ⅱ)由题意,知ξ的可能取值是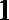
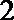
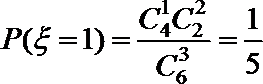
则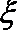
∴ 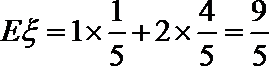
解析
解析已在路上飞奔,马上就到!
知识点
19.某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数
正确答案
(1)设甲、乙、丙中奖的事件分别为A,B,C,那么
答:甲中奖且乙、丙都没有中奖的概率是
(2)
所以中奖人数
解析
解析已在路上飞奔,马上就到!
知识点
6. 把五个标号为1到5的小球全部放入标号为1到4的四个盒子中,并且不许有空盒,那么任意一个小球都不能放入标有相同标号的盒子中的概率是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.口袋里放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,定义数列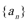

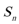
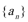
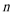
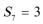
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设



(Ⅰ)求方程
(Ⅱ)求
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组





(Ⅱ)如果用分层抽样的方法从“优秀”和“良好” 的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(Ⅲ)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.五名蓝球运动员比赛前将外衣放在休息室,比赛完后都回到休息室取外衣.由于灯光暗淡,看不清自已的外衣,则至少有两人拿对自己的外衣的情况有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.某市乘公车从A站到B站所需时间(单位:分)服从正态分布N(20,202),甲上午8:00从A站出发赶往B站见一位朋友乙,若甲只能在B站上午9:00前见到乙,则甲能见到乙的概率等于_____(参考数据:


正确答案
0.9772
解析
解析已在路上飞奔,马上就到!
知识点
8.将4名志愿者分配给特奥会三个不同项目,每个项目至少分配一名自愿者,那么不同的分配方案有( )种。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率.
①若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;
②若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
正确答案
解:(1)当日需求量n≥16时,利润y=80.
当日需求量n<16时,利润y=10n-80.
所以y关于n的函数解析式为
y=
(2)①X可能的取值为60,70,80,并且P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7.
X的分布列为
X的数学期望为
EX=60×0.1+70×0.2+80×0.7=76.
X的方差为DX=(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44.
②答案一:
花店一天应购进16枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为
Y的数学期望为EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
Y的方差为DY=(55-76.4)2×0.1+(65-76.4)2×0.2+(75-76.4)2×0.16+(85-76.4)2×0.54=112.04.
由以上的计算结果可以看出,DX<DY,即购进16枝玫瑰花时利润波动相对较小.
另外,虽然EX<EY,但两者相差不大.
故花店一天应购进16枝玫瑰花.
答案二:
花店一天应购进17枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为
Y的数学期望为EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
由以上的计算结果可以看出,EX<EY,即购进17枝玫瑰花时的平均利润大于购进16枝时的平均利润.故花店一天应购进17枝玫瑰花.
解析
解析已在路上飞奔,马上就到!
知识点
17.在西部大开发中,某市的投资环境不断改善,综合竞争力不断提高,今年一季度先后有甲、乙、丙三个国际投资考察团来到该市,独立地对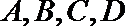
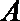
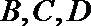
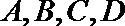
(1)求甲考察团决定到该市投资的概率;
(2)假设乙、丙考察团决定到该市投资的概率都与甲相等,记甲、乙、丙三个考察团中决定到该市投资的考察团个数为随机变量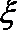
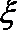
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.掷两颗均匀的骰子得两数,则事件“两数之和大于4”的概率为________。(结果用最简分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.本题(1)、(2)两个必答题。
(1)选修4-2 矩阵与变换
曲线

①求实数
②求M的逆矩阵M-1
(2)选修4-4 坐标系与参数方程
已知直线




正确答案
(1)
代入新曲线
解得
由逆矩阵公式得
(2)解法一:将圆的参数方程化为普通方程,
得
直线
即
圆心到直线的距离
所以
解法二:直线的参数方程为
将圆的参数方程化为普通方程,得
将直线的参数方程代入圆的普通方程得:

即

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析