- 概率与统计
- 共1631题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
给出下列命题:
(1)已知事件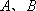
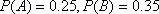
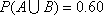
(2)已知事件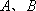
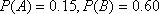
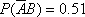
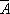
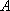
(3)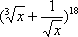
则其中真命题的序号是 [答]( )。
正确答案
解析
略
知识点
某工厂生产A,B两种元件,已知生产A元件的正品率为75%,生产B元件的正品率为80%,生产1个元件A,若是正品则盈利50元,若是次品则亏损10元;生产1个元件B,若是正品则盈利40元,若是次品则亏损5元。
(1)求生产5个元件A所得利润不少于140元的概率;
(2)设X为生产1个元件A和1个元件B所得总利润,求X的分布列和数学期望。
正确答案
见解析。
解析
知识点
在某班进行的演讲比赛中,共有
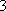

正确答案
60
解析
略
知识点
甲、乙两人参加某种选拔测试,在备选的







(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率。
正确答案
见解析
解析
(1)解:设乙答题所得分数为






乙得分的分布列如下:

(2)解:由已知甲、乙至少答对


则

故甲乙两人至少有一人入选的概率
知识点
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-
(1)求角B的大小;
(2)若a+c=1,求b的取值范围。
正确答案
(1) 

解析
(1)由已知得-cos(A+B)+cos Acos B-
即有sin Asin B-
因为sin A≠0,所以sin B-
又cos B≠0,所以tan B=
又0<B<π,所以
(2)由余弦定理,有b2=a2+c2-2accos B.
因为a+c=1,cos B=

又0<a<1,于是有

知识点
福彩中心发行彩票的目的是为了获取资金资助福利事业,现在福彩中心准备发行一种面值为5元的福利彩票刮刮卡,设计方案如下:(1)该福利彩票中奖率为50%;(2)每张中奖彩票的中奖奖金有5元,50元和150元三种;(3)顾客购买一张彩票获得150元奖金的概率为

(1)假设某顾客一次性花10元购买两张彩票,求其至少有一张彩票中奖的概率;
(2)为了能够筹得资金资助福利事业, 求
正确答案
(1)0.75
(2)
解析
(1)设至少一张中奖为事件
则
(2) 设福彩中心卖出一张彩票可能获得的资金为
则


…………………8分
所以

所以当 

所以当
知识点
观察下列等式
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
……
照此规律,第n个等式可为__________。
正确答案
12-22+32-42+…+(-1)n+1n2=(-1)n+1·
解析
第n个等式的左边第n项应是(-1)n+1n2,右边数的绝对值为1+2+3+…+n=
知识点
已知函数


(1)


(2)


正确答案
见解析。
解析
(1)










(2)直接计算知
设函数
当


因为



当




由均值不等式知,




此时存在






知识点






(1)现有该班甲、乙、丙三名同学,求这

(2)若用

正确答案
见解析
解析
(1)设“这3名同学至少有2名同学收看发射直播”为事件
则
(2)由条件可知

即



知识点
给出下列命题:
①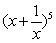
②函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积
是
③若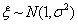
其中真命题的个数为__ 。
正确答案
1
解析
略
知识点
空气质量指数

甲、乙两城市2013年2月份中的15天对空气质量指数

(1)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(2)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(3) 在乙城市15个监测数据中任取


正确答案
见解析
解析
(1)甲城市空气质量总体较好. ………2分
(2)甲城市在15天内空气质量类别为优或良的共有10天,任取1天,空气质量类别为优或良的概率为
乙城市在15天内空气质量类别为优或良的共有5天,任取1天,空气质量类别为优或良的概率为
在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率为
………8分
(3)




数学期望
知识点
一个袋子中装有大小形状完全相同的编号分别为




(1)求取出的
(2)求取出的

(3)记


正确答案
见解析
解析
(1)解:设“取出的


答:取出的



(2)解:设“取出的


答:取出的

(3)解:





所以


知识点
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数
正确答案
见解析。
解析
(1)设甲同学在5次投篮中,有


=

(2)由题意








知识点
甲居住在城镇的








(1)请你为其选择一条由

(2)若记路线






正确答案
见解析。
解析
(1)记路段






同理:路线










路线





显然要使得由





(2)路线








所以
…………………………………………………………9分
∴

知识点
扫码查看完整答案与解析