- 概率与统计
- 共1631题
己知A、B两盒中都有红球、白球,且球的形状、大小都相同,盒子A中有m个红球与10-m个白球,盒子B中有10-m个红球与m个白球(0<m<10).
(1)分别从A、B中各取一个球,ξ表示红球的个数;
①请写出随机变量ξ的分布列,并证明E(ξ)等于定值;
②当m为何时, D(ξ)取到最小值,并求出最小值。
(2)在盒子A中不放回地摸取3个球,事件E:在第一次取到红球后,以后两次都取到白球,事件F:在第一次取到白球后,以后两次都取到红球,若概率P(E)=P(F),求m的值。
正确答案
见解析
解析
(1)分布列为:


∵1≤m≤9(m∈N*),∴当m=1或m=9,时,D(ξ)最小,最小值为
(2)
∵P(E)=P(F),∴
知识点
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为



正确答案
解析
任意找两人玩这个游戏,共有

①若












知识点
盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同。
(1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P;
(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为


正确答案
见解析。
解析
(1)一次取2个球共有

∴取出的2个球颜色相同的概率
(2)X的所有可能取值为
∴X的概率分布列为
故X的数学期望
知识点
在区间


正确答案
解析
本题是求几何概型概率,测度为长度.由


知识点
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的


(1)他们选择的项目所属类别互不相同的概率; 
(2)至少有1人选择的项目属于民生工程的概率.
正确答案
(1)
解析
解析: 记第



相互独立,
且
(1)他们选择的项目所属类别互不相同的概率
P=

(2)至少有1人选择的项目属于民生工程的概率 
P=
知识点
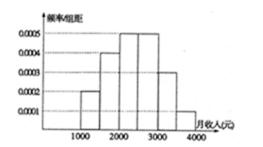
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500) 单位:元)
(1)估计居民月收入在[1500,2000)的概率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在[2500,3500)的居民数X的分布和数学期望。
正确答案
见解析。
解析
(1)依题意及频率分布直方图知,居民月收入在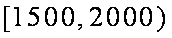
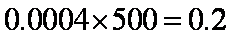
(2)频率分布直方图知,中位数在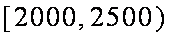
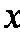
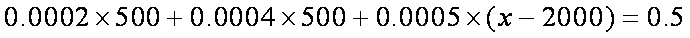
解得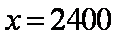
(3)居民月收入在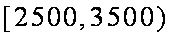
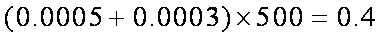
由题意知,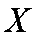
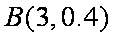
因此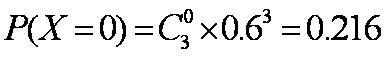
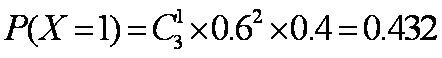
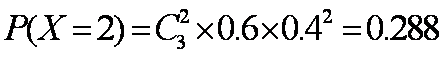
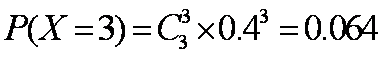
故随机变量X的分布列为
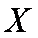
知识点
公安部最新修订的《机动车驾驶证申领和使用规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二),只有三个科目都过关后才能拿到驾驶证,某驾校现有100名新学员,第一批参加考试的20人各科目通过的人数情况如下表:
请你根据表中的数据:
(1)估计该驾校这100名新学员有多少人一次性(不补考)获取驾驶证;
(2)第一批参加考试的20人中某一学员已经通过科目一的考试,求他能通过科目二却不能通过科目三的概率;
(3)该驾校为调动教官的工作积极性,规定若所教学员每通过一个科目的考试,则学校奖励教官100元,现从这20人中随机抽取1人,记X为学校因为该学员而奖励教官的金额数,求X的数学期望。
正确答案
见解析
解析
(1)由表中数据可知一次性(不补考)获取驾驶证的频率为
估计这100名新学员中有100×
(2)设“通过科目一、二、三”分别为事件A,B,C,则P=P(B

(3)设这个学员一次性过关的科目数为Y,则Y的分布列为
EY=0×




而X=100Y,所以EX=100EY=100×
知识点
某商场在节日期间搞有奖促销活动,凡购买一定数额的商品,就可以摇奖一次,摇奖办法是在摇奖机中装有大小、质地完全一样且分别标有数字1~9的九个小球,一次摇奖将摇出三个小球,规定:摇出三个小球号码是“三连号”(如1、2、3)的获一等奖,奖1000元购物券;若三个小球号码“均是奇数或均是偶数”的获二等奖,奖500元购物券;若三个小球号码中有一个是“8”的获三等奖,奖200元购物券;其他情形则获参与奖,奖50元购物券,所有获奖等第均以最高奖项兑现,且不重复兑奖,记X表示一次摇奖获得的购物券金额。
(1)求摇奖一次获得一等奖的概率;
(2)求X的概率分布列和数学期望。
正确答案
见解析。
解析
(1)记“摇奖一次获得一等奖”为事件A,
连号的可能情况有:123,234,345,456,567,678,789共7种情况。
∴P(A)=


故摇奖一次获得一等奖的概率为
(2)由题设知X的可能取值分别为1000,500,200,50。
P(X=1000)=


P(X=200)=

P(X=50)=


∴X的分布列如下:
EX=

知识点
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有
正确答案
解析
平均数
中位数



知识点
在航天员进行的一项太空实验中,要先后实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,请问实验顺序的编排方法共有( )
正确答案
解析
本题是一个分步计数问题,
∵ 由题意知程序A只能出现在第一步或最后一步,
∴ 从第一个位置和最后一个位置选一个位置把A排列,有A21=2种结果
∵ 程序B和C实施时必须相邻,
∴ 把B和C看做一个元素,同除A外的3个元素排列,注意B和C之间还有一个排列,共有A44A22=48种结果
根据分步计数原理知共有2×48=96种结果,
故选C。
知识点
若两条异面直线所成的角为
正确答案
解析
与



























知识点
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同。
(1)若抽取后又放回,抽3次,①分别求恰2次为红球的概率及抽全三种颜色球的概率;②求抽到红球次数
(2)若抽取后不放回,抽完红球所需次数为
正确答案
见解析
解析
(1)抽1次得到红球的概率为

① 所以恰2次为红色球的概率为
抽全三种颜色的概率
② 


(2)




即分布列为:
…………11分

知识点
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分剐为1,2,3,4,从袋中任意取出3个球。
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望。
正确答案
见解析
解析
解:(1)设“取出的3个球编号都不相同”为事件A,设“取出的3个球恰有两个编号相同”为事件B,
则P(B)=


∴P(A)=1﹣P(B)=
答:取出的3个球编号都不相同的概率为
(2)X的取值为1,2,3,4。
P(X=1)=

P(X=2)=

P(X=3)=

P(X=4)=

所以X的分布列为:
X的数学期望EX=1×




知识点
高三毕业时,甲,乙,丙等五位同学站在一排合影留念,已知甲、乙相邻,则甲与丙相邻的概率为( )
正确答案
解析
由题意甲乙相邻的站法有2



知识点
对某校高三年级学生参加社区服务次数进行统计,随机抽取

(1)求出表中
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
见解析
解析
解析:(1)由分组



所以
因为频数之和为



因为


(2)因为该校高三学生有240人,分组

所以估计该校高三学生参加社区服务的次数在此区间内的人数为
(3)这个样本参加社区服务的次数不少于20次的学生共有
设在区间



则任选


而两人都在

所以所求概率为

知识点
扫码查看完整答案与解析