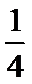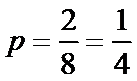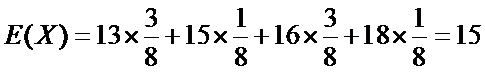- 概率与统计
- 共1631题
7.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 .
正确答案
知识点
18.(本小题满分12分)
某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
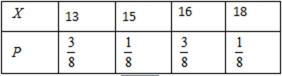
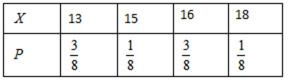
设该险种一续保人一年内出险次数与相应概率如下:
(I)求一续保人本年度的保费高于基本保费的概率;
(II)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(III)求续保人本年度的平均保费与基本保费的比值.
正确答案
知识点
7.将一个质地均匀的骰子(一种各个面上分别标有
正确答案

解析
将先后两次点数记为



考查方向
解题思路
列出所有基本事件空间以及发生事件的空间,利用比例解法求解。
易错点
列举事件的准确性。
知识点
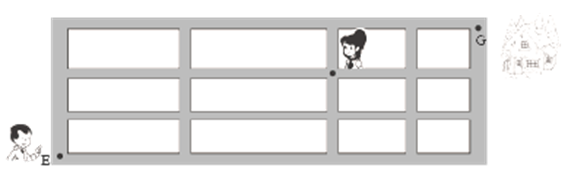
5.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
正确答案
解析
B
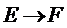
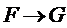
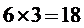
故选B.
考查方向
解题思路
从实际问题中抽出数学模型,再根据两个原理进行计算。
易错点
不能从实际问题中抽出数学模型导致出错。
知识点
19.(1)心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣 小组中按分层抽样的方法抽取50名同学(男

(1)能否据此判断有97.5% 的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5 — 7分钟,乙每次解答一道几何题所用的时间在6 - 8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率,
(3)现从选择做几何题的8名女生中
正确答案
(1)有97.5%的把握认为视觉和空间能力与性别有关;
(2)
(3)
解析
(1)由表中数据得K2的观测值
(2)设甲、乙解答一道几何题的时间分别为x、y分钟,则基本事件满足的区域为
设事件A为“乙比甲先做完此道题”则满足的区域为x>y,
∴由几何概型

(3)由题可知在选择做几何题的8名女生中任意抽取两人,抽取方法有






∴
考查方向
本题考查了独立性检验的应用;离散型随机变量的期望与方差.
解题思路
(1)根据所给的列联表得到求观测值所用的数据,把数据代入观测值公式中,做出观测值,同所给的临界值表进行比较,得到所求的值所处的位置,得到结论;
(2)利用面积比,求出乙比甲先解答完的概率;
(3)确定X的可能值有0,1,2.依次求出相应的概率求分布列,再求期望即可.
易错点
1、第一问中独立性检验知识不熟,公式不会应用;
2、第二问中几何概型转化成面积比
知识点
19.计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量
(Ⅰ)求在未来4年中,至多1年的年入流量超过120的概率;
(Ⅱ)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
若某台发电机运行,则该台发电机年利润为5000万元;若某台发电机未运行,则该台发电机年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
正确答案
(Ⅰ)
(Ⅱ)2
解析
(I)依题意


由二项分布,在未来4年中至多有1年入流量超过120的概率为:

(Ⅱ)记水电站年总利润为
由于水库年入流量总大于40,所以至少安装1台.
①安装1台发电机的情形:
由于水库年入流量总大于40,所以一台发电机运行的概率为1,
对应的年利润

②安装2台发电机的情形:
当

因此
当

因此
所以
所以
③安装3台发电机的情形:
当

因此
当

此时
当

因此
所以
所以
综上,欲使水电站年总利润的均值达到最大,应安装2台发电机.
考查方向
解题思路
(Ⅰ)先求出年入流量X的概率,根据二项分布,求出未来4年中,至少有1年的年入流量超过120的概率;
(Ⅱ)分三种情况进行讨论,分别求出一台,两台,三台的数学期望,比较即可得到.
易错点
第一问较简单,明确二项分布原理就不易出错,第二问分类出错
知识点
9.学校有两个食堂,现有3名学生前往就餐,则三个人在同一个食堂就餐的概率是_________.
正确答案
解析
利用数字代表事件,数字1表示去了一餐厅,数字2表示去了二餐厅,每组数据先后表示甲、乙、丙三人的选择,则所有可能有:
111(都去一餐厅), 112, 121, 211(有两个人去一餐厅), 122,212, 221(有一个人去一餐厅),222(都去了二餐厅)共八种可能,而满足题设条件的只有两种可能,所以
考查方向
解题思路
本题考查了古典概型,宜采用列举法求解。为做到不重不漏,最好有一定的层次顺序。
易错点
本题必须注意列举的完备性,做到不重不漏,忽视则会出现错误。
知识点
6.在二项式(

正确答案
解析
展开式的通项为
∵前三项的系数成等差数列,
∴

当


考查方向
本题主要考查了二项式定理应用、等差数列、概率
解题思路
利用二项式定理求出项数N,然后利用不相邻求概率即可
易错点
1、二项式系数和项的系数弄混淆;
2不相邻问题
知识点
16.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分。 两人4局的得分情况如下:
(Ⅰ)若从甲的4局比赛中,随机选取2局,求这2局的得分恰好相等的概率;
(Ⅱ)如果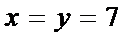
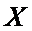
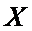
(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出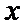
正确答案
(Ⅰ)
(Ⅱ)
(Ⅲ)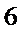

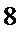
解析
试题分析:本题属于概率与统计的基本问题,题目的难点是逐渐由易到难,(1)直接按照步骤来求,(2)要注意正确求出每个变量对应的概率,(3)要注意利用离散型随机变量的分布列的性质验证分布列的正确性。
(Ⅰ)解:记 “从甲的4局比赛中,随机选取2局,且这2局的得分恰好相等”为事件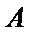
由题意,得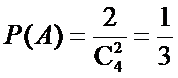
所以从甲的4局比赛中,随机选取2局,且这2局得分恰好相等的概率为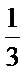
(Ⅱ)解:由题意,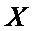
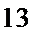
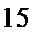
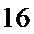

且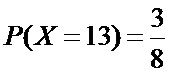
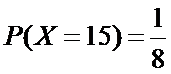
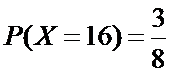
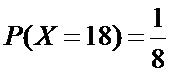
所以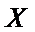
所以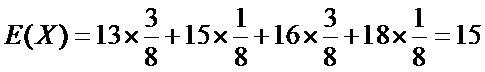
(Ⅲ)解: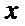
考查方向
本题主要考查了离散型随机变量的分布列、期望与方差,离散型随机变量的分布列大体有以下几类:
1.两点分布,
2.二项分布,超几何分布.
解题思路
本题考查离散型随机变量的分布列、期望与方差,解题步骤如下:
1.利用古典概型的概率公式进行求解;
2.写出随机变量的所有可能取值,分别求出每个变量对应的概率;
3.列表得到随机变量的分布列;
4.根据数学期望公式求其期望;
5.列出可能取值。
易错点
第二问中每个随机变量的概率不完全正确,导致结果错误。
知识点
18.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分. 两人4局的得分情况如下:
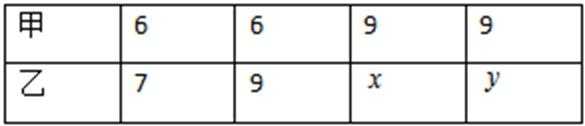
(Ⅰ)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求
(Ⅱ)如果




(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
正确答案
(Ⅰ)15
(Ⅱ)

(Ⅲ) 


解析
(Ⅰ)解:由题意,得

因为在乙的4局比赛中,随机选取1局,则此局得分小于6分的概率不为零,
所以
又因为

所以
所以
(Ⅱ)解:设 “从甲、乙的4局比赛中随机各选取1局,且得分满足
记甲的4局比赛为



为



则从甲、乙的4局比赛中随机各选取1局,所有可能的结果有16种, 它们是:















而事件








因此事件

(Ⅲ)解:



考查方向
解题思路
1、第一问由选取1局得分小于6分的概率不为零,可知x,y取值均为小于或等于5的自然数;结合乙的平均得分高于甲的平均得分确定的
2、第二问通过列举从甲、乙的4局比赛中随机各选取1局,所有可能的结果可以找出满足题意的事件数目,最终求出其概率。
3、第三问通过平均分相同得出

易错点
不能从题目中提取出

知识点
4.袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球。从袋中任取2个球,所取的2个球中恰有
正确答案
解析
从袋中任取








考查方向
解题思路
先算出从所有球中选出两个球会出现的所有情况,再算出恰有一白一红球出现的所有情况。
易错点
组合数的计算容易出错。
知识点
18. 某卫视的大型娱乐节目现场,所有参演的节目都由甲、乙、丙三名专业老师投票决定是否通过进入下一轮,甲、乙、丙三名老师都有“通过”“待定”“淘汰”三类票各一张,每个节目投票时,甲、乙、丙三名老师必须且只能投一张票,每人投三类


(I)求某节目的投票结果获“通过”的概率;
(II)记某节目投票结果中所含“通过”和“待定”票票数之和为X,求X的分布列和数学期望.
正确答案
(1)
(2)2
解析
试题分析:本题属于离散型随机变量应用中的基本问题,题目的难度是逐渐由易到难
(Ⅰ)设“某节目的投票结果获“通过”为事件A,
则事件A包含该节目获2张“通过票”或该节目获3张“通过票”,
∵甲、乙、丙三名老师必须且只能投一张票,每人投三类票中的任意一类票的概率为
且三人投票相互没有影响,∴某节目的投票结果是最终获“通过”的概率为:
(Ⅱ)所含“通过”和“待定”票票数之和




∴

考查方向
解题思路
本题考查离散型随机变量应用,解题步骤如下:
(1)设“某节目的投票结果是最终获一等奖”为事件A,则事件A包含该节目可以获2张“获奖票”或该节目可以获3张“获奖票”,由此能求出某节目的投票结果是最终获一等奖的概率.
(2)所含“获奖”和“待定”票数之和X的值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望.
易错点
1、第一问中弄清事件类型
2、第二问中计算不正确得不到正确结论。
知识点
7.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球中有黄球的概率为___________
正确答案
解析
考查方向
解题思路
本题考查运用乘法原理求这2只球中没有黄球的概率,再利用互斥事件的性质求解。解题步骤如下:
易错点
本题必须注意审题,忽视则会出现错误。
知识点
23.为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加。现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名。从这8名运动员中随机选择4人参加比赛.
(1)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件A发生的概率;
(2)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望.
正确答案
见解析
解析
(1)由已知,有
所以事件

(2)随机变量
所以随机变量
所以随机变量
考查方向
解题思路
1利用已知条件把“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会的组合数求出,进而求出概率
易错点
本题必须注意审题,否则求解错误。
知识点
3.书架上有


正确答案
解析
这是一个古典概率问题.概率值为一个分式.用列举法求解。分母是样本点总数,为:从5本书中任意抽取两本,总的基本事件总数为10个,分子为事件的样本点数,为:5本书中任意抽取两本数学书,其基本事件总数为6个,所以取出的两本书都是数学书的概率为
考查方向
解题思路
求解古典概型问题,关键是准确地计算出总的基本事件个数,和所要求的事件包含的基本事件个数。
易错点
对基本事件总数不能准确地计算出。
知识点
扫码查看完整答案与解析