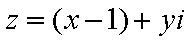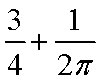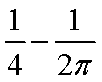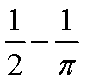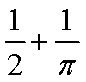- 概率与统计
- 共1631题









正确答案
解析
任取不同的两个点

符合要求的有序点对

∴符合要求的点

考查方向
解题思路
先确定分母,八个点任取不同的两个点的种数为


易错点
枚举法寻找符合要求的有序点对
知识点
13.如图,点





正确答案
解析
由已知得阴影部分面积为

考查方向
解题思路
分别求出矩形和阴影部分的面积,利用几何概型公式,解答。
易错点
不会运用导数和积分求不规则图形的面积
知识点

6.由不等式组确定的平面区域记为Ω1,不等式组确定的平面区域为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
正确答案
解析
画出两个区域所表示的图形如图所示,




考查方向
解题思路
画出图形,算出面积,进而求出概率.
易错点
易错点是,容易把图形画错.
知识点
8.分别在区间


正确答案
解析
根据题意作图
基本事件空间区域的面积为

∴
考查方向
解题思路
该题解题思路
1)题意画出满足条件的区域,以及不等式
2)求出矩形区域面积和利用定积分求
3)使用几何概型公式计算出概率
易错点
主要易错于几何概型的形式出错,定积分求措
知识点
4.如图,在正方形

正确答案
知识点
4.如图,在正方形

正确答案
解析
由题意可知,正方形的面积为1
阴影部分的面积
所以由集合概型可以知道,选B
考查方向
几何概型求概率
易错点
不会计算阴影部分的面积
教师点评
利用几何概型求概率关键在于求不规则图形的面积
知识点
14.如图,圆






正确答案
解析
余弦函数

而圆O:
根据几何概型的概率公式可知点A落在区域M内的概率是
故答案为
考查方向
解题思路
先利用定积分求出余弦函数y=cosx的图象与x轴围成的区域M的面积,以及圆的面积,再利用几何概型的概率公式求出点A落在区域M内的概率即可.
易错点
几何概型具有两大特点:一是试验的可能的结果为无限个;二是试验的结果在一个区域内均匀分布。解题的关键是判断试验的结果在哪个区域内是均匀的。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
11.设复数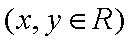
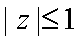
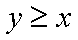
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
① 每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题A、B、C、D顺序作答,直至答题结束。
假设甲同学对问题A、B、C、D回答正确的概率依次为



(1)求甲同学能进入下一轮的概率;
(2)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。
正确答案
见解析。
解析
设A、B、C、D分别为第一、二、三、四个问题,用






所以 
(1)记“甲同学能进入下一轮”为事件
则 
由于每题答题结果相互独立,因此


(2)由题意,随机变量
由于每题答题结果相互独立,
所以,
因此 随机变量
所以
知识点
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示。
已知这100位顾客中的一次购物量超过8件的顾客占55%。
(1)确定

(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过
正确答案
(1)

(2)
解析
(1)由已知,得
该超市所有顾客一次购物的结算时间组成一个总体,所以收集的100位顾客一次购物的结算时间可视为总体的一个容量随机样本,将频率视为概率得

X的数学期望为

(2)记A为事件“该顾客结算前的等候时间不超过2.5分钟”,


由于顾客的结算相互独立,且

故该顾客结算前的等候时间不超过2.5分钟的概率为
知识点
两个实习生每人加工一个零件,加工为一等品的概率分别为

否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为
正确答案
解析
记两个零件中恰好有一个一等品的事件为A,则
P(A)=P(A1)+ P(A2)=
知识点
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的利润不少于10万元的概率。
正确答案
见解析。
解析
(1)由题设知,X的可能取值为10,5,2,-3,且
P(X=10)=0.8×0.9=0.72, P(X=5)=0.2×0.9=0.18,
P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02。
由此得X的分布列为:
(2)设生产的4件甲产品中一等品有

由题设知

又


所求概率为
答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
知识点
已知甲盒中仅有1个球且为红球,乙盒中有m个红球和n个篮球

(a)放入

(b)放入

则 ( )
正确答案
解析


∴


故
又∵
∴
又
∴
=



所以
知识点
扫码查看完整答案与解析