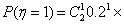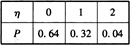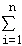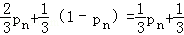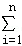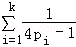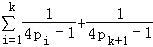- 概率与统计
- 共1631题
某单位为绿化环境,移栽了甲、乙两种大树各




(1)求
(2)求甲种大树成活的株数大于乙种大树成活的株数的概率;
(3)用



正确答案
见解析。
解析
设“甲种大树恰有


设“乙种大树恰有


(1)两种大树各成活

(2)设“甲种大树成活的株数大于乙种大树成活的株数”为事件
则
所以,甲种大树成活的株数大于乙种大树成活的株数的概率为
(3)由题意知,

所以


知识点
某学校的一间功能室统一使用某种节能灯管,已知这种灯管的使用寿命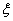
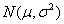
(1)求这种灯管的平均使用寿命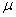
(2)假设一间功能室一次性换上2支这种新灯管,使用12个月时进行一次检查,将已经损坏的灯管换下(中途不更换),设需要更换的灯管数为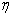
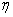
正确答案
见解析。
解析
(1)因为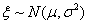
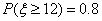
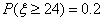
所以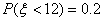
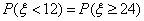
由正态分布密度曲线的对称性可知,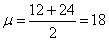
即这种灯管的平均使用寿命是18个月,(6分)
(2)这种灯管的使用寿命少于12个月的概率为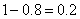
由题意知,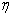
则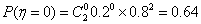
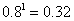
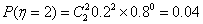
所以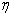
所以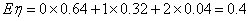
知识点
中国航母“辽宁舰”是中国第一艘航母,“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性,科学家对蒸汽轮机进行了170余项技术改进,增加了某项新技术,该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测,假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为


(1)求该项技术量化得分不低于8分的概率;
(2)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望。
正确答案
见解析。
解析
(1)该项新技术的三项不同指标甲、乙、丙独立通过检测合格分别为事件


则事件“得分不低于8分”表示为

























(2)该项新技术的三个指标中被检测合格的指标个数




























随机变量






知识点
深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球),每次训练,都从中任意取出2个球,用完后放回。
(1)设第一次训练时取到的新球个数为

(2)求第二次训练时恰好取到一个新球的概率。
正确答案
见解析。
解析
(1)
设“第一次训练时取到










(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件
则“第二次训练时恰好取到一个新球”就是事件
而事件


所以,
由条件概率公式,得



所以,第二次训练时恰好取到一个新球的概率为

知识点
从棱长为1的正方体的8个顶点中任取不同2点,设随机变量ξ是这两点间的距离。
(1)求概率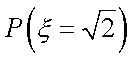
(2)求ξ的分布列,并求其数学期望E(ξ)。
正确答案
见解析。
解析
(1)从正方体的8个顶点中任取不同2点,共有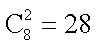
因为正方体的棱长为1,所以其面对角线长为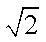
正方体每个面上均有两条对角线,所以共有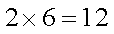
因此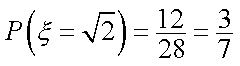
(2)随机变量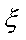
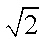
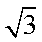
正方体的棱长为1,而正方体共有12条棱,于是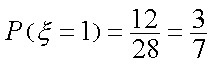
从而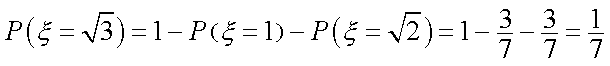
所以随机变量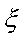
因此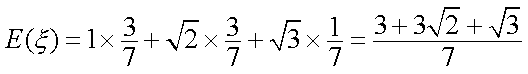
知识点
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功,已知在6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为

正确答案
见解析。
解析
(1)设甲、乙闯关成功分别为事件A、B,
则

事件
则甲、乙至少有一人闯关成功的概率是

(2)由题知


则
所以
知识点
为迎接2013年“两会”(全国人大3月5日-3月18日、全国政协3月3日-3月14日)的胜利召开,某机构举办猜奖活动,参与者需先后回答两道选择题,问题A有四个选项,问题B有五个选项,但都只有一个选项是正确的,正确回答问题A可获奖金

正确答案
见解析。
解析
该参与者随机猜对问题A的概率
随机猜对问题B的概率
回答问题的顺序有两种,分别讨论如下:
①先回答问题A,再回答问题B,参与者获奖金额

则


数学期望
②先回答问题B,再回答问题A,参与者获奖金额

则


数学期望

于是,当

当

当

知识点
某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四
项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试。已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为
(1)求该生被录取的概率;
(2)记该生参加考试的项数为

正确答案
见解析。
解析
(1)若该生被录取,则前四项最多有一项不合格,并且第五项必须合格
记A={前四项均合格}
B={前四项中仅有一项不合格}
则P(A)=
P(B)=
又A、B互斥,故所求概率为
P=P(A)+P(B)=
(2)该生参加考试的项数



……………………………………10分

知识点
在一个盒子中有分别标有数字1,2,3,4,5的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之积为偶数的概率是 。
正确答案
解析
从标有数字1,2,3,4,5的5张卡片中一次取出2张卡片,共有
其中取到的卡片上的数字之积为偶数分为两种情况:一类是取得的两个数字都是偶数:只有一种情况(2,4);
另一类是一个偶数和一个奇数,有
∴取到的卡片上的数字之积为偶数的概率P=
知识点
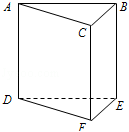
如图,一颗棋子从三棱柱的一个顶点沿棱移到相邻的另一个顶点的概率均为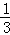
(1)求p1,p2的值;
(2)求证: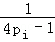
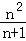
正确答案
见解析
解析
(1)棋子在上底面点A处,若移了n次后,棋子落在上底面顶点,棋子从A出发,由3条路径,所以p1=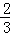
棋子移动两次,还在上底面时,有两种可能,p2=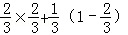
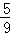
(2)因为移了n次后,棋子落在上底面顶点的概率为pn。
故落在下底面顶点的概率为1﹣pn。
于是,移了n+1次后,棋子落在上底面顶点的概率记为pn+1=
,从而pn+1﹣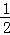
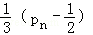
所以数列{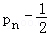
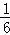
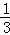
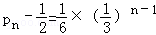
用数学归纳法证明: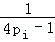
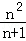
①当n=1时左式=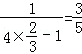
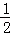
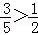
当n=2时,左式=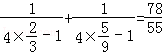
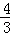
②假设n=k(k≥2)不等式成立,即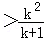
则n=k+1时,左式=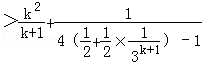
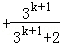
要证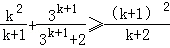
只要证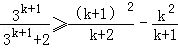
即证: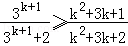
只要证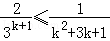
只要证3k+1≥2k2+6k+2,
因为k≥2,所以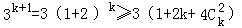
所以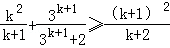
即n=k+1时不等式也成立,由①②可知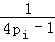
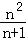
知识点
一批产品共100件,其中有3件不合格品,从中随机抽取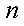
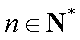
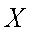
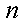
(1)若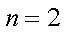
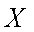
(2)求使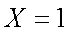
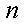
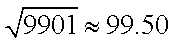
正确答案
见解析。
解析
(1)当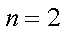
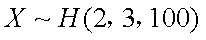
则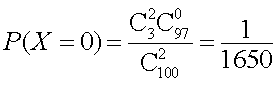
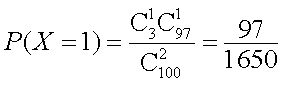
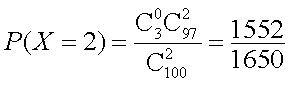
所以,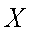
(2)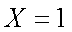
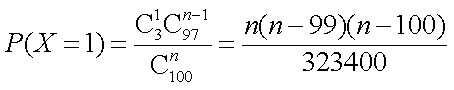
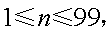
记函数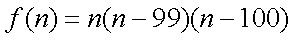
则由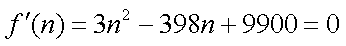
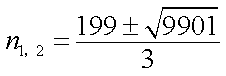
由参考数据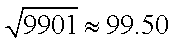
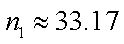
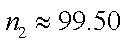
而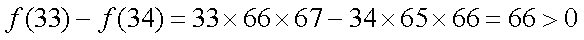
结合函数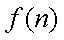
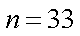
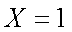
知识点
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”),为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[15,25),[25,35)的被调查者中各随机选取3人进行追踪调查,记选中的6人中不赞成“国五条”的人数为X,求随机变量X的分布列及数学期望。
正确答案
见解析
解析
解析:(1)这

(2)根据频率分布直方图可知







∴
∴
知识点
已知矩阵M=
(1)求实数a,b的值;
(2)求曲线C′的方程。
正确答案
(1)∴
(2)
解析
(1)由已知得M



∴
(2)设点P(x',y')是曲线C:xy=1上的任意一点,变换后的点为P'(x,y)
则



因为x′y′=1,所以

知识点
我省某示范性高中为推进新课程改革,满足不同层次学生的要求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座(规定:各科达到预先设定的人数时称为满座,否则称为不满座),统计数据表明,各学科讲座各天的满座概率如下表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为

正确答案
见解析
解析
解析:(1)设数学辅导讲座在周一、周三、周五都不满座为事件

(2)







所以,随机变量

故
知识点
如图,设







正确答案
解析
将








知识点
扫码查看完整答案与解析