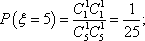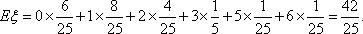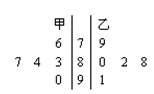- 茎叶图
- 共46题
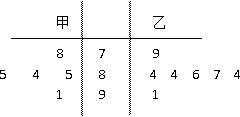
为迎接2012年伦敦奥运会,在著名的海滨城市青岛举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛的得分如茎叶图所示:
(1)若从甲运动员的每轮比赛的得分中任选3个不低于80且不高于90的得分,求甲的三个得分与其每轮比赛的平均得分的差的绝对值都不超过2的概率;
(2)若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个,求甲、乙两名运动员得分之差的绝对值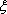
正确答案
见解析
解析
(1)由茎叶图知,甲运动员七轮比赛的得分情况为:78,81,84,85,84,85,91,所以甲每轮比赛的平均得分为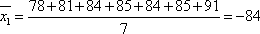
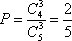
(2)设甲、乙两名运动员的得分分别为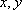
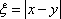
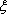
当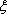

当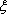
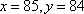

当
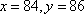
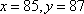
当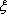
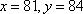
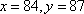
当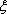
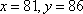
当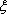
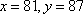
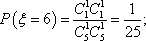
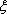
知识点
如图是甲、乙两名同学进入高中以来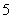
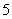
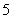
正确答案
84;2
解析
略
知识点
下图是









(注:标准差


正确答案
解析
略
知识点
为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是

正确答案
解析
解:由茎叶图知,
甲的平均数是
乙的平均数是
∴乙的平均数大于甲的平均数,
从茎叶图可以看出乙的成绩比较稳定,
故选D。
知识点
某商品,根据以往资料统计,顾客采用的付款期数
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元。
(1)求事件

(2)求

正确答案
见解析。
解析
(1)由
知


(2)








知识点
中国
若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有湖北师范学院的“高个子”才能担任“兼职导游”。
(1)根据志愿者的身高编茎叶图指出湖北师范学院志愿者身高的中位数;
(2)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(3)若从所有“高个子”中选3名志愿者,用


正确答案
见解析
解析
解析:(1)根据志愿者的身高编茎叶图知湖北师范学院志愿者身高的中位数为:
……………………2分
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,



则至少有1人为高个子的概率
……………………6分
(3)由题可知:湖北师范学院的高个子只有3人,则
故



即






……………12分
知识点
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高,现从一批数量很大的罗非鱼中随机地抽出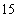
《中华人民共和国环境保护法》规定食品的汞含量不得超过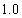
(1)检查人员从这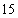
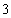
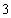
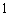
(2)若从这批数量很大的鱼中任选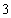
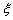
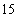
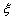

正确答案
见解析
解析
(1)记“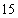
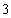
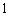
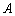
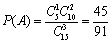
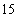
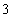
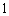
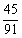
(2)依题意可知,这批罗非鱼中汞含量超标的鱼的概率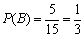
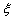
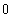
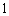
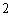
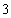
则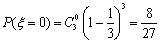
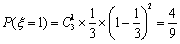
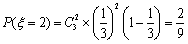
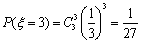
其分布列如下:
…………………………12分
所以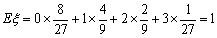
知识点
空气质量指数

甲、乙两城市2013年2月份中的15天对空气质量指数

(1)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(2)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(3) 在乙城市15个监测数据中任取


正确答案
见解析
解析
(1)甲城市空气质量总体较好. ………2分
(2)甲城市在15天内空气质量类别为优或良的共有10天,任取1天,空气质量类别为优或良的概率为
乙城市在15天内空气质量类别为优或良的共有5天,任取1天,空气质量类别为优或良的概率为
在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率为
………8分
(3)




数学期望
知识点
右图是甲,乙两组各








正确答案
解析
略
知识点
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以
已知甲、乙两个小组的数学成绩的平均分相同。
(1)求
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为

正确答案
见解析
解析
(1)解:依题意,得

(2)解:根据已知条件,可以求得两组同学数学成绩的平均分都为
方差为
(3)解:分别从甲、乙两组同学中各随机选取一名同学,共有
这两名同学成绩之差的绝对值
所以
由表可得







所以随机变量
随机变量

知识点
扫码查看完整答案与解析