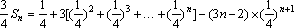- 运用诱导公式化简求值
- 共45题
11.已知:



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
一个几何体的三视图如图所示,其中主视图和左视图 是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为 ( )
正确答案
解析
略。
知识点
如图,在直角梯形









①当


②

③

其中所有正确结论的序号是_________.
正确答案
2,3
解析
略
知识点
在数列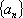
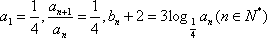
(1)求数列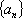
(2)求证:数列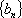
(3)设数列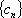

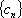
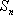
正确答案
见解析。
解析
(1)∵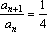
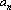


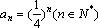
(2)∵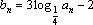
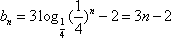
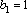
公差d=3,∴数列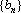
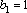
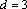
(3)由(1)、(2)知,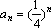

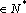
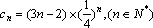
∴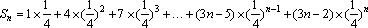
于是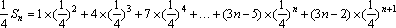
两式①-②相减得
=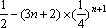
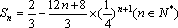
知识点
已知二次函数



(1)求a的值;
(2)

(3)若m=1,且x>0,求证:
正确答案
见解析。
解析
(1)解:∵关于


即不等式

∴
∴
∴
∴
(2)解法1:由(1)得
∴

∴
方程

①当

则



∴函数


∴函数

②当



若
故

∴函数

∴函数
若
则





∴函数



∴函数


综上所述, 当



当




(其中

解法2:由(1)得
∴

∴
若函数


令
得
则
方程(*)的两个实根为

设
①若



则



∴函数


∴函数

②若

又由(**)解得

故
则





∴函数



∴函数


综上所述, 当



当




(其中

(2)证法1:∵

∴

令
则

∵
∴

∴

证法2:下面用数学归纳法证明不等式
① 当


② 假设当


则

也就是说,当
由①②可得,对


知识点
扫码查看完整答案与解析