- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
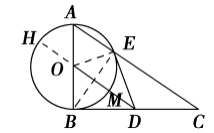
在△ABC中,


(1)求△ABC的面积

正确答案
(1)3(2)
解析
(1)在
所以
根据余弦定理得:
而

所以
(2)由(1)可知
所以
知识点
已知





(1)求sinθ的值;
(2)求tan2θ的值。
正确答案
见解析。
解析
(1)∵


∵

∴
∴sinθ=



(2)由

两边平方得:

∵

∴


∴

知识点
在三角形ABC中,角A、B、C 的对边长分别为
(1)求角B的值;
(2)若
正确答案
(1)
解析
解析:(1)由正弦定理得
……………………………………2分


(2)



知识点
如图,曲线





(1) 求
(2) 求四边形


正确答案
(1)
解析
(1) 联立曲线





(2)设



则
令


设
则令
可得当



此时


联立曲线




所以




则直线

当




即对角线



知识点
已知


正确答案
解析
略
知识点
在ABC中,若tanAtanB= tanA+tanB+1,则cosC的值是
正确答案
解析
由





知识点
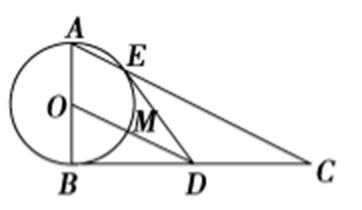
如图,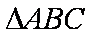
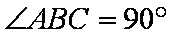
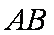

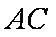
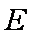
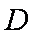
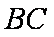
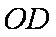

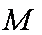
(1)求证:
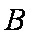
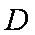
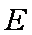
(2)求证: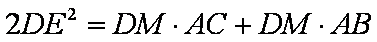
正确答案
见解析。
解析
(1)证明:如图,连结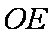
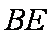
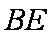
又∵D是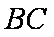
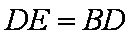
又∵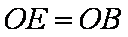
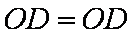
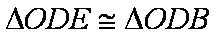
∴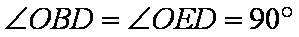

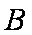

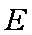
(2)证明:延长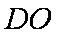

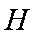
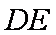

∴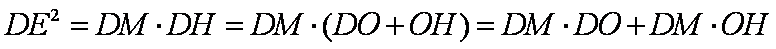
∴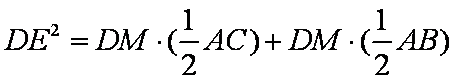
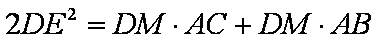
知识点
在△ABC中,内角A、B、C的对边长分别为a、b、c,已知

则b=
正确答案
4
解析
略
知识点
已知


正确答案
解析
略
知识点
在三角形

(1) 求角
(2) 若


正确答案
(1)
解析
(1) 由



则




(2)因为


当



当

所以由

所以
综上可知
知识点
扫码查看完整答案与解析