三角函数的概念、同角三角函数的关系式和诱导公式
共714题

三角函数的概念、同角三角函数的关系式和诱导公式
共714题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

在△ABC中，tan＝2sinC。

（1）求∠C的大小；

（2）若AB＝1，求△ABC周长的取值范围。

正确答案

（1）（2）

解析

解析：（1）由及，得，

（2）由正弦定理，得，△ABC的周长

所以周长的取值范围是（2,3］

知识点

任意角的概念

题型：简答题

简答题 · 14 分

已知抛物线上点到焦点的距离为.

（1）求抛物线方程；

（2）点为准线上任意一点，为抛物线上过焦点的任意一条弦，设直线，，的斜率为，，，问是否存在实数，使得恒成立.若存在，请求出的值；若不存在，请说明理由。

正确答案

见解析

解析

（1）

（2）设直线：，与联立，消去，整理得：

，设，，有

易知，而

所以存在实数，使得恒成立.

知识点

任意角的概念

题型：单选题

单选题 · 5 分

如图，在等腰直角△ABC中，AB=AC=3，点D在边BC上且BD=DC,点P是线段AD上任一点，则的取值范围是

正确答案

解析

分别以为轴建立直角坐标系，则，，设，，，所以

知识点

任意角的概念

题型：单选题

单选题 · 5 分

下面四个条件中，使a>b成立的充分而不必要的条件是（）

正确答案

解析

因为若，则a>b一定成立；而a>b成立，不一定成立。因此选项A为a>b成立的充分而不必要条件。

知识点

任意角的概念

题型：填空题

填空题 · 5 分

已知中，点的坐标分别为则的面积为

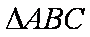
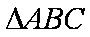
正确答案

解析

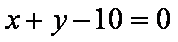
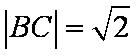
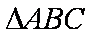
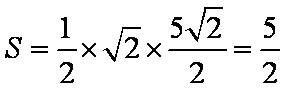
直线BC方程为，，点A到直线BC 的距离为，所以的面积。

知识点

任意角的概念

题型：简答题

简答题 · 14 分

在△ABC中，角A、B、C的对边分别为a、b、c且.

（1）若，求角B的大小；

（2）若

正确答案

见解析

解析

（1）

由正弦定理，得，∴ ，∴ （舍）。

（2）

由（1）中得或，又，∴ ，∴ 。

∴ ，∴ 当时，取最小值。

知识点

任意角的概念

题型：简答题

简答题 · 12 分

已知角的终边上一点，且，求及。

正确答案

见解析。

解析

…………………………………6分

当时，………………………………… 9分

当时，…………………………………12分

知识点

任意角的概念

题型：简答题

简答题 · 12 分

如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，四边形ABCD为菱形，△PAD为正三角形，,E、F分别为PA、BC的中点。

（1）求证：平面PCD；

（2）求三棱锥E-PDC的体积.

正确答案

见解析。

解析

（1）

取线段AD的中点G，连接FG、EG，由已知可得FG//PD,EG//DC

又∵∴ 平面PCD

（2）连接PG,∴PG⊥AD，∵平面PAD⊥平面ABCD

∴PG⊥平面ABCD，∴PG为三棱锥P-ECD的高，

知识点

任意角的概念

题型：简答题

简答题 · 14 分

已知中，为角A,B,C所对的边，。

（1）求的值；

（2）若的面积为，且边上的中线的长为，求，的长。

正确答案

见解析

解析

解：（1）由正弦定理得：

（2）由题意得：，即：

由余弦定理得：，即：

联立上述两式,解得：或.

知识点

任意角的概念

题型：简答题

简答题 · 15 分

如图在三棱柱ABC-中，平面，D是棱

（1）求证：

（2）求二面角的正切值。

正确答案

见解析

解析

（1）

证明：平形四边形中，，，且是棱CC1的中点，

∴，且，又∵平面平面，平面平面，∴平面，

又平面，∴

（2）解：过作，垂足为，连接。

由（1）已得，∴平面，

∴为二面角的平面角，又，∴在中，。

∴二面角的正切值是。

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 三角函数的图象与性质

百度题库 > 高考 > 文科数学 > 三角函数的概念、同角三角函数的关系式和诱导公式

扫码查看完整答案与解析