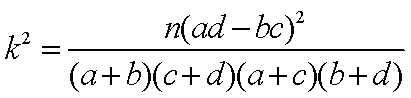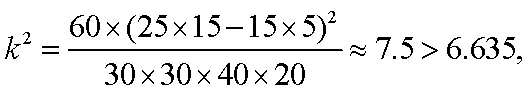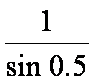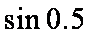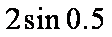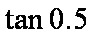- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象,为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
参考数据:
参考公式:
(1)根据表中数据,求出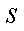
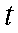
(2)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
正确答案
见解析。
解析
(1)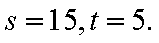
假设:是否使用淡化海砂与混凝土耐久性是否达标无关,由已知数据可求得:
因此,能在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关,………(6分)
(2)用分层抽样的方法在使用淡化海砂的样本中抽取了6个,其中应抽取“混凝土耐久性达标”的为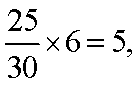
“混凝土耐久性达标”的记为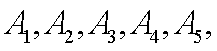
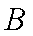
从这6个样本中任取2个,共有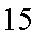
设“取出的2个样本混凝土耐久性都达标”为事件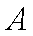
它的对立事件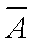
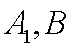
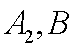
(
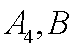
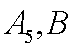
所以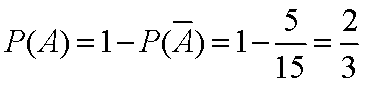
则取出的2个样本混凝土耐久性都达标的概率是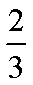
知识点
已知三角形





(1)求角
(2)设


正确答案
(1)60○
(2)[1,2)
解析
(1)∵



∴

(2)∵
∴
∴


∴


知识点

正确答案
解析
知识点
如图,在圆O中,直径AB与弦CD垂直,垂足为E,


正确答案
解析
易知:
知识点
在




(1)若

(2)若

正确答案
(1)
(2)
解析
(1)由已知



由


由


(2)因为
所以

由此得


其面积
知识点
如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点。
(1) 求证:AC⊥BC1;
(2) 求证:AC1∥平面CDB1;
(3) 求异面直线AC1与B1C所成角的余弦值。
正确答案
见解析。
解析
(1)证明:在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,
∴AC⊥BC
又∵C1C⊥AC.∴AC⊥平面BCC1B1
∵BC1⊂平面BCC1B,∴AC⊥BC1
(2)证明:设CB1与C1B的交点为E,连接DE,
又四边形BCC1B1为正方形。
∵D是AB的中点,E是BC1的中点,∴DE∥AC1
∵DE⊂平面CDB1,AC1⊄平面CDB1,
∴AC1∥平面CDB1

(3)解:∵DE∥AC1,
∴∠CED为AC1与B1C所成的角。
在△CED中,


∴
∴异面直线AC1与B1C所成角的余弦值为
知识点
经研究发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散.设



(1)求出k的值,并指出讲课开始后多少分钟,学生的注意力最集中?能坚持多久?
(2)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到185,那么经过
适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
正确答案
见解析。
解析
(1)当t=20时,f(t)=240,则有:240=20k+400
∴k=-8
当t∈(0,10]时,f(t)=-t2+26t+80是单调递增的,且f(10)=240,
当t∈[10,20]时,f(t)=240,
当t∈[20,40]时,f(t)=-8t+400是单调递减的,且f(20)=240,
∴当课开始10分钟后,学生的注意力最集中,能持续10分钟。
(2)由f(t)=-t2+26t+80=185可得t1=5,t2=21(舍去),
由f(t)=-8t+400=185可得t=26.875,
即熊讲课后5分钟到26.875分钟这段时间内学生的注意力不低于185,
则学生的注意力最低保持在185的时间为26.875-5=21.875<25,
所以不能在所需状态下讲解完这道题目。
知识点
若方程

正确答案
解析
把方程









知识点
如果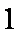
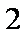
正确答案
解析
易知圆的半径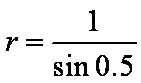
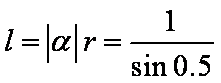
知识点
已知



正确答案
解析
因为







知识点
扫码查看完整答案与解析