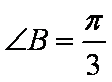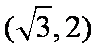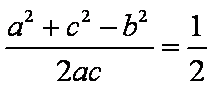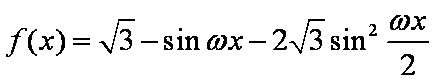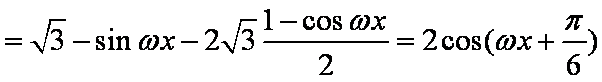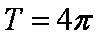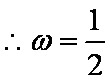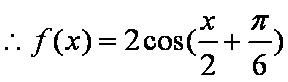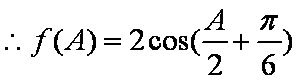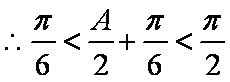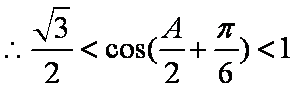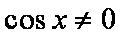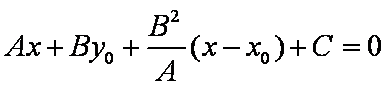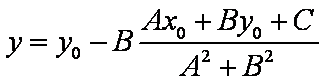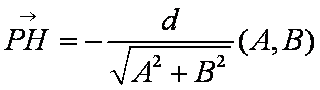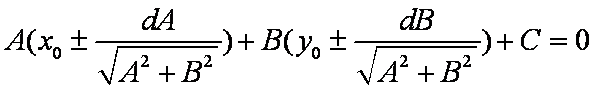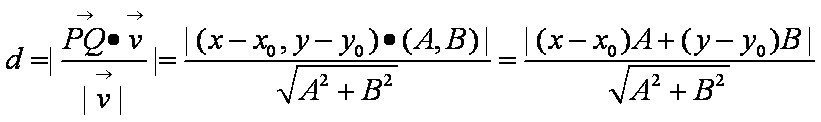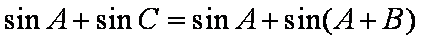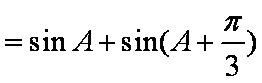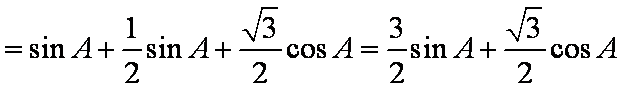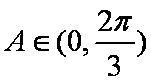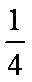- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
设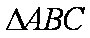
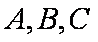
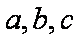
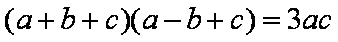
(1)求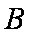
(2)若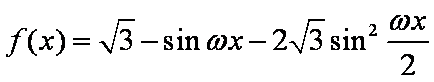

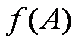
正确答案
(1)
(2)
解析
(1)由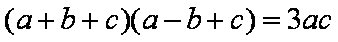
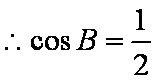
(2)
由题意可知函数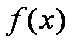

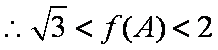
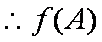
知识点
如图,已知正三棱柱






(1) 求证:
(2) 若D为线段CE的中点,求二面角
正确答案
见解析。
解析
(1)证明:由题易知

又
又

又
又
(2)由题意易求


又



在




知识点
已知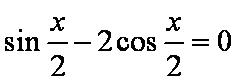
(1)求
(2)求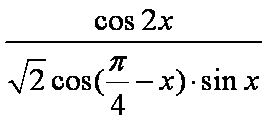
正确答案
见解析
解析
(1)由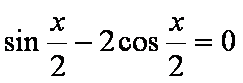
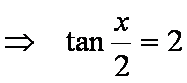
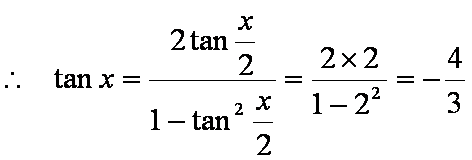
(2) 由(1)知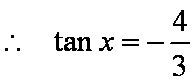
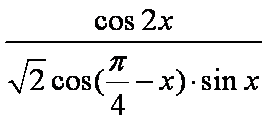
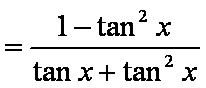

知识点
若

正确答案
解析


知识点
设点P的坐标为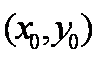
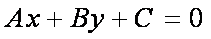

正确答案
见解析
解析
点P到直线l的距离公式为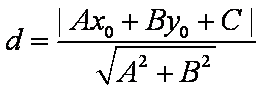
证法1:过点P作直线l的垂线,垂足为H,若A = 0,则直线l的方程为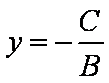

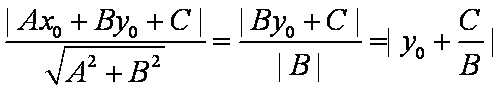
若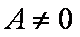
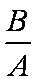
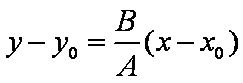
解得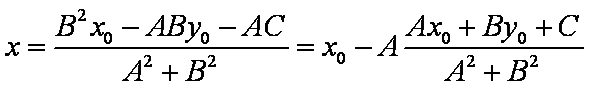
据两点间距离公式得
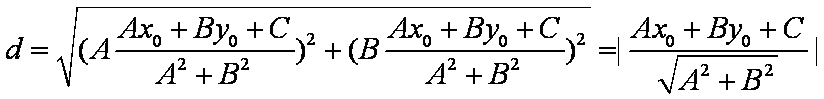
证法2:若B = 0,则直线l的方程为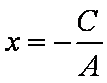
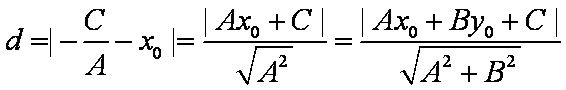
若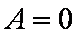
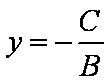
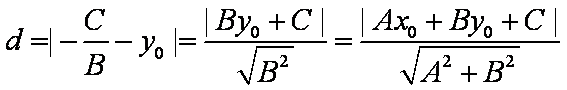
若
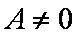

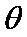

因为 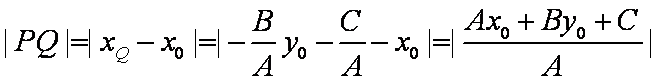
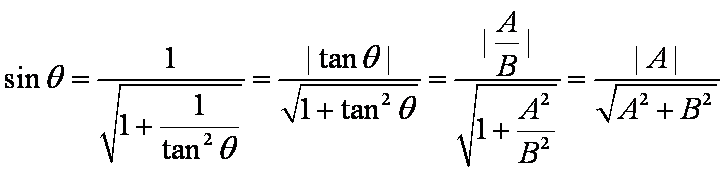
所以,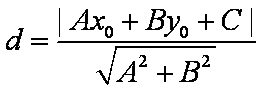


证法3:过点P作直线l的垂线,垂足为H,则直线PH的一个方向向量对应于直线l的一个法向量,而直线l的一个法向量为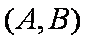
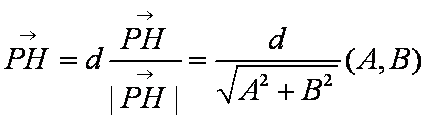
设点H的坐标为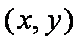
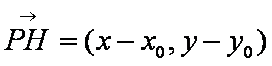
把点H的坐标代入直线l的方程得
整理得 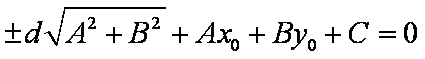
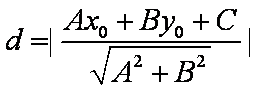
证法4:过点P作直线l的垂线,垂足为H,在直线l上任取一点Q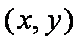
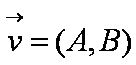
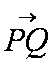

因为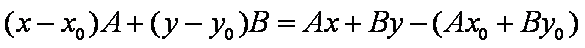
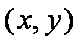

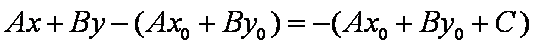
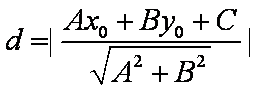
知识点
在



(1)求角
(2)若


正确答案
见解析。
解析
(1)由题意得:
有
故
(2)由(1)知
又
因此
知识点
已知离心率



(1)求椭圆
(2)过原点




正确答案
见解析
解析
(1)∵
∴
故椭圆
(2)若直线



将



∴
∴
又点


∴
① 当

② 当

③ 当

若直线



综上,

知识点
三角形的三个内角A、B、C所对边的长分别为
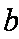
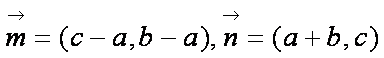
若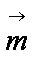
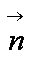
(1)求角B的大小;
(2)求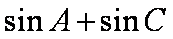
正确答案
见解析
解析
解(1)由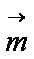
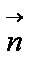
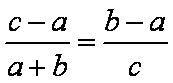
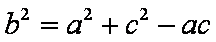
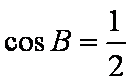

(2)

因为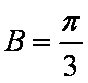
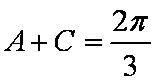
所以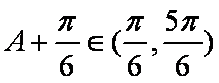
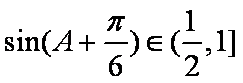
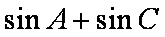
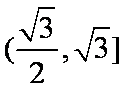
知识点
在△ABC中,

(1)求sinC的值;
(2)设BC=5,求△ABC的面积。
正确答案
见解析。
解析
(1)在⊿ABC中,∵

又∵


(2)由正弦定理知:
∴
知识点
sin15○cos15○=
正确答案
解析
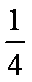
知识点
扫码查看完整答案与解析