三角函数的概念、同角三角函数的关系式和诱导公式
共714题

三角函数的概念、同角三角函数的关系式和诱导公式
共714题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

8.设△ABC的内角A, B, C所对的边分别为a, b, c, 若, 则△ABC的

形状为( )

A直角三角形

B锐角三角形

C钝角三角形

D不确定

正确答案

解析

略。

知识点

任意角的概念

题型：简答题

简答题 · 10 分

18.如图，在等腰直角三角形中，，，点在线段上。

（1）若，求的长；

（2）若点在线段上，且，问：当取何值时，的面积最小？并求出面积的最小值。

正确答案

见解析。

解析

（1）在中，，，，

由余弦定理得，，

得，

解得或。

（2）设，，

在中，由正弦定理，得，

所以，

同理

故

因为，，所以当时，的最大值为，此时的面积取到最小值，即2时，的面积的最小值为。

知识点

任意角的概念

题型：单选题

单选题 · 5 分

6.设等边三角形ABC边长为6，若，则等于（）

C- 18

D18

正确答案

解析

由题意可得

知识点

任意角的概念

题型：简答题

简答题 · 12 分

17.在等比数列中，

（1）求数列的通项公式；

（2）令求数列的前项和

正确答案

（1）

（2）

解析

（1）设等比数列的公比为依题意得解得

所以：数列的通项公式

（2）由（1）得

知识点

任意角的概念

题型：简答题

简答题 · 14 分

在△ABC中，a,b,c分别为内角A,B,C的对边，且2cos(B-C)=4sinBsinC-1。

（1）求A；

（2）若a=3，，求b。

正确答案

（1）A=

（2）

解析

（1）由2cos(B-C)=4sinBsinC-1，

得2(cosBcosC+sinBsinC)-4sinBsinC=-1，

即2(cosBcosC-sinBsinC)=-1。

从而2cos(B+C)=-1，得cos(B+C)=，

∴B+C=,故A=。

（2）由，得，

∴，

∵，∴，解得

知识点

任意角的概念

题型：简答题

简答题 · 12 分

17.设的内角的对边分别为，满足．

（1）求角的大小；

（2）若，，求的面积．

正确答案

见解析。

解析

（1）由已知及正弦定理可得，

整理得，

所以．

又，故．

（2）由正弦定理可知，又，，，

所以．

又，故或．

若，则，于是；

若，则，于是．

知识点

任意角的概念

题型：填空题

填空题 · 5 分

12.已知，，则（用，表示）．

正确答案

解析

略

知识点

任意角的概念

题型：简答题

简答题 · 12 分

18.如图，三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，AA1=A1C=AC=2，AB=BC且AB⊥BC.

（1）求证：AC⊥A1B；

（2）求三棱锥C1﹣ABA1的体积．

正确答案

见解析。

解析

（1）证明：取AC中点O，连A1O，BO.

∵AA1=A1C，∴A1O⊥AC，

又AB=BC，∴BO⊥AC，

∵A1O∩BO=O，∴AC⊥平面A1OB，

又A1B⊂平面A1OB，

∴AC⊥A1B

（2）解：由条件得：

∵三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，

AA1=A1C=AC=2，AB=BC且AB⊥BC，

∴，，

∴=

=．

知识点

任意角的概念

题型：单选题

单选题 · 5 分

4.若tanα＞0，则（　　）

Asinα＞0

Bcosα＞0

Csin2α＞0

Dcos2α＞0

正确答案

解析

∵tanα＞0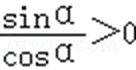，∴，则sin2α=2sinαcosα＞0.故选C。

知识点

任意角的概念

题型：填空题

填空题 · 5 分

14.若△ABC的面积为，BC=2，C=，则边AB的长度等于_________.

正确答案

解析

，所以，又，，所以是等边三角形，于是。

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 三角函数的图象与性质

百度题库 > 高考 > 文科数学 > 三角函数的概念、同角三角函数的关系式和诱导公式

扫码查看完整答案与解析