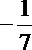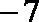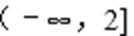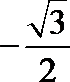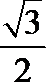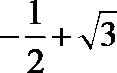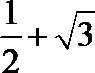- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
3．已知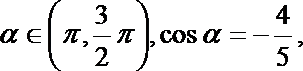
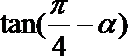
A7
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．在
正确答案
直角三角形
解析
解析已在路上飞奔，马上就到！
知识点
9．若函数f（x）=cos2x+asinx在区间（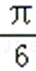
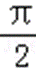
正确答案
解析
解：由f（x）=cos2x+asinx
=﹣2sin2x+asinx+1，
令t=sinx，
则原函数化为y=﹣2t2+at+1．
∵ x∈（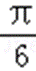
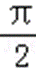
则y=﹣2t2+at+1在t∈（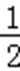
∵ y=﹣2t2+at+1的图象开口向下，且对称轴方程为t=
∴ 
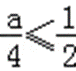
∴ a的取值范围是（﹣∞，2]．
故答案为：（﹣∞，2]．
知识点
18．如图，四棱锥P-ABCD的底面ABCD是平行四边形，PA⊥底面ABCD，∠PCD＝90°，PA =AB=AC．
（I）求证：AC⊥CD;
（II）点E在棱PC的中点，求点B到平面EAD的距离．
正确答案
（I）证明：
因为PA⊥ 底面ABCD，所以PA⊥ CD，
因为∠ PCD＝90°，所以PC⊥ CD，
所以CD⊥ 平面PAC，
所以CD⊥ AC．
（II）因为PA＝AB＝AC＝2，E为PC的中点，
所以AE⊥ PC，AE＝
由（I）知AE⊥ CD，
所以AE⊥ 平面PCD．
作CF⊥ DE，交DE于点F，
则CF⊥ AE，则CF⊥ 平面EAD．
因为BC∥ AD，所以点B与点C到平面EAD的距离相等，
CF即为点C到平面EAD的距离．
在Rt△ ECD中，CF＝
所以，点B到平面EAD的距离为
解析
解析已在路上飞奔，马上就到！
知识点
9．在区间
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．在△ABC 中，已知角A、B、C 所对的三条边分别是
（1）求证：
（2）求函数
正确答案
（1）因为
所以
（2）
因为
所以
所以
所以
解析
解析已在路上飞奔，马上就到！
知识点
1．
A
B
C
D
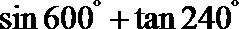
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．tan（－30）°的值为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．设点M是线段
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知a．b．c分别是△ABC的三个内角A．B．C
正确答案
1
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析