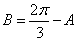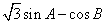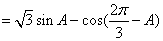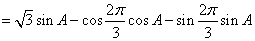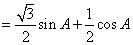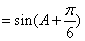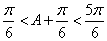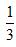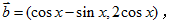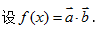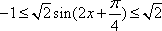- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
在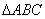
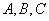
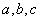
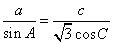
(1)求角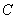
(2)求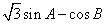
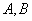
正确答案
见解析。
解析
(1)由条件结合正弦定理得,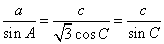
从而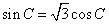
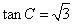
∵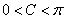
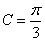
(2)由(1)知
∴
∵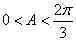
当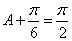
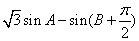
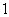
此时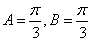
知识点
已知




(1)求
(2)设

正确答案
(1)
(2)
解析
(1)∵


∴

∴

(2)由(1)知,
∴
∵


∴
知识点
在△






(1)求证:
(2)求
正确答案
见解析
解析
解析:(1)由已知,
得
由基本不等式

所以

(2)
………………9分
由(1),


所以,

知识点
已知


正确答案
解析
略
知识点
如图所示,角A为钝角,且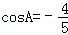
(1)已知AP=5,AQ=2,求PQ的长;
(2)设∠APQ=α,∠AQP=β,且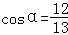
正确答案
见解析
解析
(1)∵A是钝角,cosA=﹣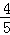
在△APQ中,由余弦定理得PQ2=AP2+AQ2﹣2AP•AQcosA,
∴PQ2=52+22﹣2×5×2×(﹣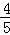
∴PQ=3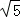
(2)∵α为三角形的角,cosα=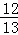
∴sinα=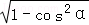
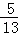
又sin(α+β)=sin(π﹣A)=sinA=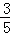
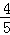
∴sin(2α+β)=sin[α+(α+β)]=sinαcos(α+β)+cosαsin(α+β)=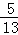
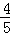
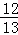
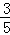
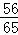
知识点
如果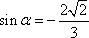
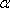
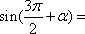
正确答案
解析
略
知识点
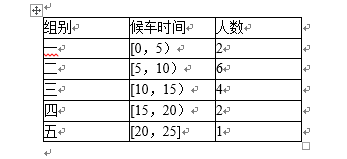
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:min):
(1)求这15名乘客的平均候车时间;
(2)估计这60名乘客中候车时间少于10分钟的人数;
(3)若从上表第三、四组的6人中选2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率。
正确答案
见解析。
解析
解:(1)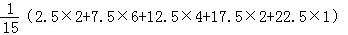
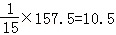
(2)候车时间少于10分钟的概率为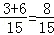
所以候车时间少于10分钟的人数为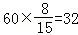
(3)将第三组乘客编号为a1,a2,a3,a4,第四组乘客编号为b1,b2。
从6人中任选两人有包含以下15个基本事件:
(a1,a2),(a1,a3),(a1,a4),(a1,b1),(a1,b2),
(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),
(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2),
其中两人恰好来自不同组包含8个基本事件,所以,所求概率为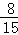
知识点
已知向量
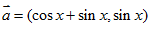
(1)求函数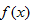
(2)当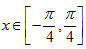
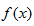
正确答案
见解析。
解析
(1)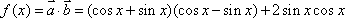
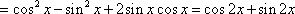
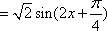
所以函数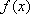
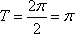
(2)当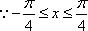
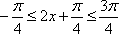
∴当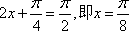
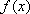
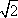
当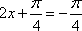
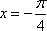
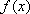
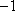
知识点
对大于或等于






根据上述分解规律,则


正确答案
9
解析
略
知识点
已知点


正确答案
解析
略
知识点
扫码查看完整答案与解析