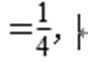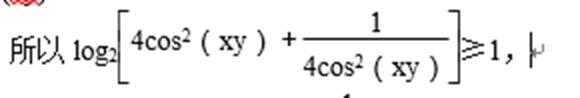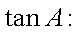- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
在△ABC中,角A,B,C所对的边分别为a,b,c,且
(1)求B;
(2)若
正确答案
见解析。
解析
(1)由

所以


因为在△ABC中,sinA≠0,sinC≠0,
所以cosB=
因为B(0,π),所以
(2)因为

因为

所以
=
知识点
在△ABC中,若9cos2A﹣4cos2B=5,则
正确答案

解析
在△ABC中,∵9cos2A﹣4cos2B=5,∴9(1﹣2sin2A )﹣4(1﹣2sin2B)=5,
化简可得 9sin2A=4sin2B,故有 

由正弦定理可得 


故答案为 
知识点
若实
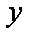
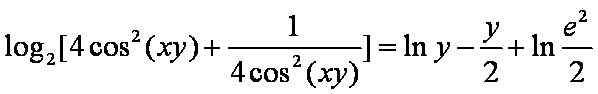
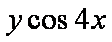
正确答案
-1
解析
设f(y) =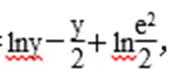

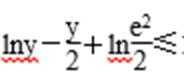
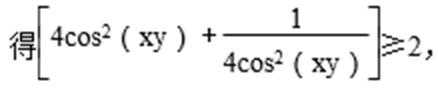
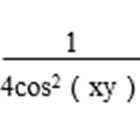
所以log2[4cos2(xy) 
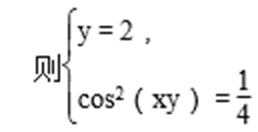

知识点
如图,正五边形





正确答案
解析
因为














知识点
如图,在等腰三角形ABC中,底边BC=2,





正确答案
0
解析
∵在等腰三角形ABC中,底边BC=2,∴可取BC的中点O作为坐标原点距离平面直角坐标系。
则B(﹣1,0),C(1,0),
设A(0,a)(a>0),∵

∴


∵



∴
∵




∴
∴


故答案为0。
知识点
在△ABC中,若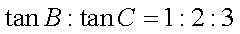
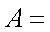
正确答案
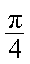
解析
设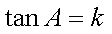
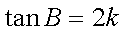
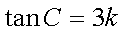
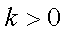
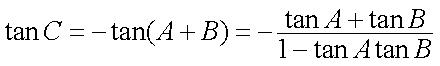
求得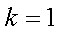
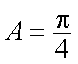
知识点
在△ABC中,角A,B,C的对边分别为a,b,c。
(1)若cos(A+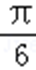
(2)若cosA=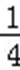
正确答案
见解析
解析
(1)在△ABC中,若cos(A+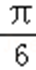
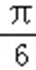
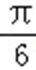
化简可得
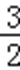

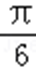
(2)若cosA=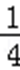
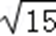
由于sinA=

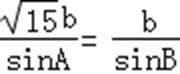
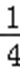
知识点
已知命题p:函数

命题q:方程

若命题“p或q”是假命题,求实数a的取值范围。
正确答案
解析
解析:当p为真时,
q为真时 ,a=0 不符合条件
当


即


即

“p或q”假,即p假且q假




知识点
某工厂有216名工人,现接受了生产1000台GH型高科技产品的总任务。已知每台GH型产品由4个G型装置和3个H型装置配套组成,每个工人每小时能加工6个G型装置或3个H型装置。现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组)。设加工G型装置的工人有x人,他们加工完G型装置所需时间为g(x),其余工人加工完H型装置所需时间为h(x)(单位:小时,可不为整数)
(1)写出g(x),h(x)的解析式;
(2)写出这216名工人完成总任务的时间f(x)的解析式;
(3)应怎样分组,才能使完成总任务用的时间最少?
正确答案
见解析
解析
解析:(1)由题意知,需加工G型装置4000个,加工H型装置3000个,所用工人分别为



即



(2)
∵ 0<x<216,∴216-x>0,
当



当




(3)完成总任务所用时间最少即求
当


∴

当


∴

∴
∴ 加工G型装置,H型装置的人数分别为86、130或87、129。 ………14分
知识点
已知函数
(1)若


(2)求
(3)设




正确答案
见解析。
解析
(1)由已知

故曲线


(2)
①当


所以,

②当


在区间



所以,函数


……………….8分
(3)由已知,转化为

由(2)知,当



(或者举出反例:存在
当



故

所以

知识点
扫码查看完整答案与解析